Master Math Fast with LCM GCD Prime Numbers Worksheets

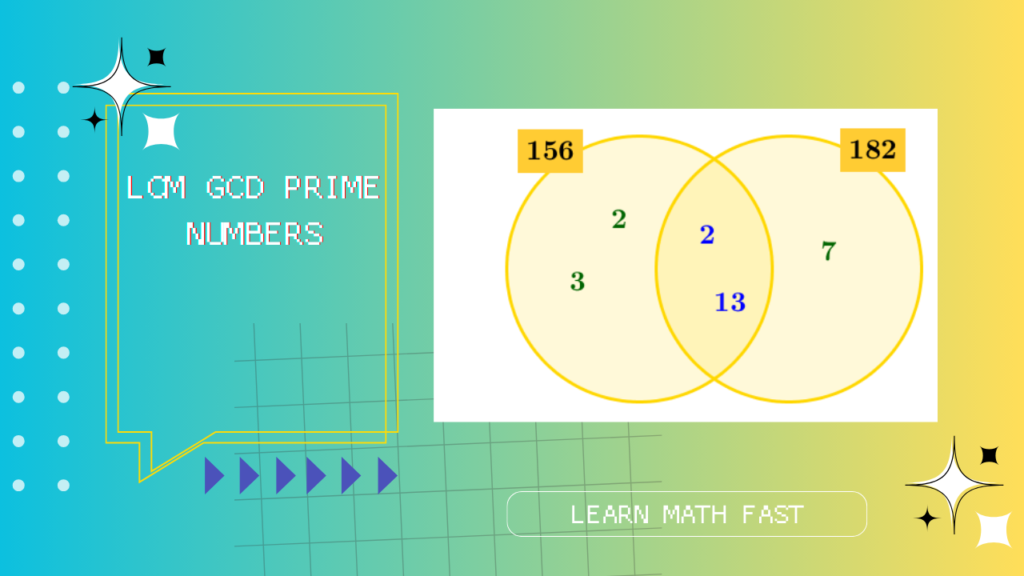
let’s discuss the LCM (Least Common Multiple), GCD (Greatest Common Divisor) and prime numbers.

A multiple of a natural number is the product of this number by another natural number.

Example; Multiples of 6: 0, 6, 12, 18, 24, 30, 36, 42, 48, 54, 60…….

A divisor of a natural number is a natural that divides it exactly.

Example: Divisors of 6: 1, 2, 3, 6

Attention! 0n cannot divide by 0

Least Common Multiple (LCM)

The LCM of two or more numbers is the smallest multiple that is evenly divisible by each of those numbers. To calculate the LCM of two numbers, you can use the formula:

LCM(a, b) = (a * b) / GCD(a, b)

For example, to find the LCM of 12 and 18:

LCM(12, 18) = (12 * 18) / GCD(12, 18)

Greatest Common Divisor (GCD)

The GCD of two or more numbers is the largest number that evenly divides each of those numbers. You can use the Euclidean algorithm to find the GCD of two numbers.

For example, the GCD of 24 and 36 is calculated as follows:

GCD(24, 36) = GCD(36, 24)
GCD(36, 24) = GCD(24, 12)
GCD(24, 12) = GCD(12, 0)
GCD(12, 0) = 12

GCD(24, 36) = 12.

List of Prime Numbers

Prime numbers are natural numbers greater than 1 that have no positive divisors other than 1 and themselves. Here is a list of prime numbers up to 100:

2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97

These are some of the prime numbers, and there are infinitely many more prime numbers as you go further into larger numbers.

Relationship Between GCD and LCM

The relationship between GCD and LCM is given by the formula:

LCM(a, b) = (a * b) / GCD(a, b)

This formula allows you to calculate the LCM of two numbers if you know their GCD.

Example:

Let’s find the GCD and LCM of two numbers, say 12 and 18.

GCD(12, 18) = 6 (because the largest number that divides both 12 and 18 evenly is 6)

LCM(12, 18) = (12 * 18) / 6 = 36 (using the formula)

Applications:

GCD and LCM are used in various mathematical and computational problems, including simplifying fractions, solving equations, and optimizing algorithms.

Prime Numbers and GCD/LCM:

Prime numbers have a GCD of 1 with any other number (except for themselves).

When you calculate the LCM of two prime numbers, the result is simply their product because there are no common factors other than 1.

Example:

Let’s find the GCD and LCM of two prime numbers, say 5 and 7.

GCD(5, 7) = 1 (because prime numbers have no common factors)

LCM(5, 7) = 5 * 7 = 35 (the product of the prime numbers)

Difference between GCD and LCM

The greatest common divisor (GCD), also known as the highest common factor (HCF), is the largest number that is a divisor of two or more numbers. The least common multiple (LCM) is the smallest number that is divisible by two or more numbers.

Characteristic	GCD	LCM
Definition	The largest number that is a divisor of two or more numbers.	The smallest number that is divisible by two or more numbers.
Formula	$GCD (a, b) = HCF (a, b) = max {d ∣ d divides a and d divides b}$	$LCM (a, b) = min {m ∣ m is divisible by a and m is divisible by b}$
Example	$GCD (12, 18) = 6$	$LCM (12, 18) = 36$

Here is a simple analogy to help you understand the difference between GCD and LCM:

Imagine you have a bag of apples and a bag of oranges. The GCD of the number of apples and oranges is the largest number that you can divide both bags of fruit by evenly. The LCM of the number of apples and oranges is the smallest number of apples and oranges that you need in order to have the same number of apples and oranges in each bag.

For example, if you have 12 apples and 18 oranges, the GCD of 12 and 18 is 6. This means that you can divide both bags of fruit by 6 and have the same number of apples and oranges in each bag (i.e., 2 apples and 3 oranges). The LCM of 12 and 18 is 36. This means that you need to have 36 apples and 36 oranges in order to have the same number of apples and oranges in each bag.

How to find LCM and GCD

There are two main methods for finding the LCM:

Prime factorization: This method is more efficient than the listing multiples method, but it requires some knowledge of prime factorization. To find the LCM of two or more numbers using this method, first prime factorize each number. Then, the LCM of the numbers is the product of the highest powers of each prime factor that appears in any of the numbers.

For example, to find the LCM of 6 and 10, we can prime factorize each number as follows:

6 = 2 * 3
10 = 2 * 5

The LCM of 6 and 10 is the product of the highest powers of 2 and 3 that appear in any of the numbers, which is 2^1 * 3^1 * 5^1 = 30.

Listing multiples: This method is straightforward, but it can be time-consuming for large numbers. To find the LCM of two or more numbers using this method, simply list the multiples of each number until you find a number that is divisible by all of the other numbers.

For example, to find the LCM of 6 and 10, we can list the multiples of each number as follows:

Multiples of 6: 6, 12, 18, 24, 30, ...
Multiples of 10: 10, 20, 30, ...

The first number that is divisible by both 6 and 10 is 30. Therefore, the LCM of 6 and 10 is 30.

Finding the GCD

There are also two main methods for finding the GCD:

Prime factorization: To find the GCD of two or more numbers using this method, first prime factorize each number. Then, the GCD of the numbers is the product of the lowest powers of each prime factor that appears in any of the numbers.

For example, to find the GCD of 6 and 10, we can prime factorize each number as follows:

6 = 2 * 3
10 = 2 * 5

The GCD of 6 and 10 is the product of the lowest powers of 2 and 3 that appear in any of the numbers, which is 2^1 * 3^0 = 2.

Euclidean algorithm: This algorithm is a more efficient way to find the GCD of two large numbers. It is based on the following principle: the GCD of two numbers is equal to the GCD of the larger number and the remainder when the larger number is divided by the smaller number.

To find the GCD of two numbers using the Euclidean algorithm, follow these steps:

Divide the larger number by the smaller number.
If the remainder is zero, then the GCD is the smaller number.
If the remainder is not zero, then the GCD is the GCD of the smaller number and the remainder.

Repeat steps 2 and 3 until the remainder is zero. The last non-zero remainder is the GCD of the two numbers.

For example, to find the GCD of 6 and 10, we can use the Euclidean algorithm as follows:

10 / 6 = 1 with a remainder of 4
6 / 4 = 1 with a remainder of 2
4 / 2 = 2 with a remainder of 0

Therefore, the GCD of 6 and 10 is 2.

Both of these methods can be used to find the LCM and GCD of any number, regardless of how many numbers you are trying to find the LCM and GCD for.

LCM GCD Prime Numbers Worksheet With Answers

For each pair of prime numbers, calculate the LCM and GCD. Write your answers in the provided spaces.

Pair: 2, 3

LCM: __________

GCD: __________

Pair: 5, 7

LCM: __________

GCD: __________

Pair: 11, 13

LCM: __________

GCD: __________

Pair: 17, 19

LCM: __________

GCD: __________

Pair: 23, 29

LCM: __________

GCD: __________

Pair: 31, 37

LCM: __________

GCD: __________

Pair: 41, 43

LCM: __________

GCD: __________

Pair: 47, 53

LCM: __________

GCD: __________

Pair: 59, 61

LCM: __________

GCD: __________

Pair: 67, 71

LCM: __________

GCD: __________

Pair: 83, 89

LCM: __________

GCD: __________

Pair: 103, 107

LCM: __________

GCD: __________

Answers:

Pair: 2, 3

LCM: 6

GCD: 1

Pair: 5, 7

LCM: 35

GCD: 1

Pair: 11, 13

LCM: 143

GCD: 1

Pair: 17, 19

LCM: 323

GCD: 1

Pair: 23, 29

LCM: 667

GCD: 1

Pair: 31, 37

LCM: 1147

GCD: 1

Pair: 41, 43

LCM: 1763

GCD: 1

Pair: 47, 53

LCM: 2491

GCD: 1

Pair: 59, 61

LCM: 3599

GCD: 1

Pair: 67, 71

LCM: 4757

GCD: 1

Pair: 83, 89

LCM: 7387

GCD: 1

Pair: 103, 107

LCM: 11021

GCD: 1

Determine if the following numbers are prime or composite: a) 17 b) 12 c) 31 d) 9 e) 23

Answers:

a) Prime b) Composite c) Prime d) Composite e) Prime

Find the GCD of the following pairs of numbers:

a) GCD(8, 12)

b) GCD(15, 25)

c) GCD(18, 27)

d) GCD(35, 49)

e) GCD(14, 28)

Answers: 2. a) 4 b) 5 c) 9 d) 7 e) 14

Find the LCM of the following pairs of numbers: a) LCM(6, 8) b) LCM(9, 15) c) LCM(20, 25) d) LCM(12, 18) e) LCM(36, 48)

Answers: 3. a) 24 b) 45 c) 100 d) 36 e) 144

Determine the LCM and GCD of the following pairs of numbers: a) LCM(10, 15), GCD(10, 15) b) LCM(7, 11), GCD(7, 11) c) LCM(24, 36), GCD(24, 36)

Answers:

a) LCM = 30, GCD = 5

b) LCM = 77, GCD = 1

c) LCM = 72, GCD = 12

A classroom has 24 desks, and another classroom has 18 desks. What is the least number of students for which they can equally distribute the desks? Find the GCD.

Answers:

The least number of students is found by calculating the GCD of 24 and 18. GCD(24, 18) = 6. So, they can equally distribute the desks among 6 students.

Arithmetic course and exercises