Multiples and divisors course for beginners

Multiples and divisors are two closely related terms in mathematics. A non-zero natural number ‘b’ is a divisor of an integer ‘a’ if and only if ‘a’ is a multiple of ‘b’.
Multiples are numbers that are divisible by another number. For example, 12, 24, and 36 are all multiples of 6, because they are all divisible by 6.
Divisors are numbers that divide into another number without a remainder. For example, 2, 3, and 4 are all divisors of 12, because they all divide into 12 without a remainder.
Every number has an infinite number of multiples, but a finite number of divisors. For example, the multiples of 6 are 6, 12, 18, 24, 30, 36, 42, 48, and so on. The divisors of 12 are 1, 2, 3, 4, 6, and 12.
Properties of multiples and divisors
- Every number is a multiple of itself.
- Every number is a divisor of itself.
- If a is a multiple of b and b is a multiple of c, then a is also a multiple of c.
- If a is a divisor of b and c is a divisor of b, then a is also a divisor of c.
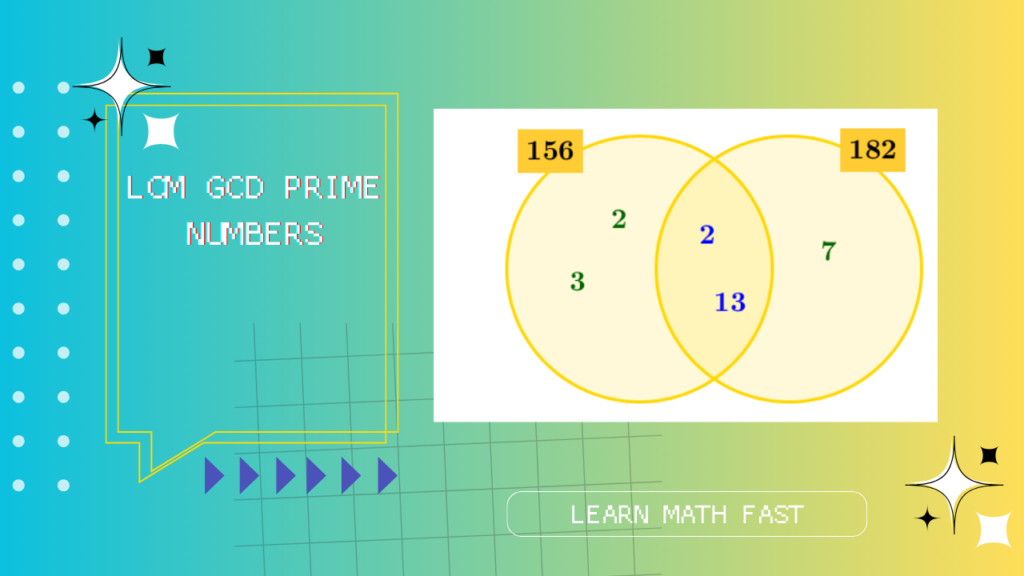
- The least common multiple (LCM) of two or more numbers is the smallest number that is a multiple of all of the given numbers.
- The greatest common divisor (GCD) of two or more numbers is the largest number that is a divisor of all of the given numbers.
- The smallest positive divisor of a number is always 1, and the largest is the number itself.
- If two numbers have a common divisor (other than 1), they are said to have a “common factor.
Multiples and divisors are related because if ‘b’ is a multiple of ‘a,’ then ‘a’ is a divisor of ‘b,’ and vice versa.
Multiples and divisors examples
Multiples Examples:
1. Multiples of 4:
– Multiples of 4 are obtained by multiplying 4 by integers:
– 4, 8, 12, 16, 20, 24, 28, …
2. Multiples of 7:
– Multiples of 7 are obtained by multiplying 7 by integers:
– 7, 14, 21, 28, 35, 42, 49, …
3. Multiples of 10:
– Multiples of 10 are obtained by multiplying 10 by integers:
– 10, 20, 30, 40, 50, 60, 70, …
Divisors Examples:
1. Divisors of 12:
– Divisors of 12 are the numbers that can evenly divide 12 without remainder:
– 1, 2, 3, 4, 6, 12
2. Divisors of 15:
– Divisors of 15 are the numbers that can evenly divide 15 without remainder:
– 1, 3, 5, 15
3. Divisors of 24:
– Divisors of 24 are the numbers that can evenly divide 24 without remainder:
– 1, 2, 3, 4, 6, 8, 12, 24
Relationship Between Multiples and Divisors:
1. If 15 is a multiple of 5, then 5 is a divisor of 15.
– Multiples: 15 = 5 x 3
– Divisors: 5 divides 15 evenly.
2. If 10 is a multiple of 2, then 2 is a divisor of 10.
– Multiples: 10 = 2 x 5
– Divisors: 2 divides 10 evenly.
Least Common Multiple (LCM) Example:
Let’s find the LCM of 6 and 8:
1. List the multiples of 6: 6, 12, 18, 24, 30, …
2. List the multiples of 8: 8, 16, 24, 32, 40, …
The LCM is the smallest common multiple, which in this case is 24. So, LCM(6, 8) = 24.
Common Divisors Example:
Find the common divisors of 18 and 24:
1. Divisors of 18: 1, 2, 3, 6, 9, 18
2. Divisors of 24: 1, 2, 3, 4, 6, 8, 12, 24
The common divisors are the numbers that appear in both lists, which are 1, 2, 3, 6. So, the common divisors of 18 and 24 are 1, 2, 3, and 6.
These multiples and divisors examples demonstrate how multiples and divisors work and how they relate to each other in various mathematical contexts.
Difference between factor and divisor
The terms factor and divisor are often used interchangeably, but there is a subtle difference between the two.
A factor of a number is a number that divides evenly into that number. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12.
A divisor of a number is a number that can be divided into that number with no remainder. For example, the divisors of 12 are 1, 2, 3, 4, and 6.
In other words, all factors of a number are also divisors of that number, but not all divisors of a number are factors of that number. For example, 5 is a divisor of 12, but it is not a factor of 12 because it does not divide evenly into 12.
| Term | Definition | Example |
|---|---|---|
| Factor | A number that divides evenly into another number | The factors of 12 are 1, 2, 3, 4, 6, and 12. |
| Divisor | A number that can be divided into another number with no remainder | The divisors of 12 are 1, 2, 3, 4, 6, and 12. |
Difference between multiple and factor
A multiple of a number is a number that is divisible by that number without a remainder. For example, 12, 24, and 36 are all multiples of 6, because they are all divisible by 6 without a remainder.
A factor of a number is a number that divides evenly into that number. For example, 2, 3, and 6 are all factors of 6, because they all divide evenly into 6.
The main difference between a multiple and a factor is that a multiple is a product of a number, while a factor is a divisor of a number. In other words, a multiple is a number that is obtained by multiplying a number by itself one or more times, while a factor is a number that divides a number evenly.
Here is a table that summarizes the key differences between multiples and factors:
| Characteristic | Multiple | Factor |
|---|---|---|
| Definition | A number that is divisible by another number without a remainder | A number that divides evenly into another number |
| Relationship to the given number | Product | Divisor |
| Example | 12, 24, and 36 are all multiples of 6 | 2, 3, and 6 are all factors of 6 |
Multiples and divisors worksheets
Worksheet 1: Multiples
1. Find the first five multiples of the following numbers:
– 3
– 7
– 12
– 9
– 5
2. Determine whether the following statements are true or false:
– 18 is a multiple of 6.
– 25 is a multiple of 3.
– 14 is a multiple of 5.
– 10 is a multiple of 2.
– 21 is a multiple of 7.
Worksheet 2: Divisors
1. List all the divisors of the following numbers:
– 24
– 15
– 36
– 8
– 10
2. Determine whether the following statements are true or false:
– 4 is a divisor of 16.
– 9 is a divisor of 27.
– 6 is a divisor of 14.
– 12 is a divisor of 48.
– 7 is a divisor of 49.
Worksheet 3: Multiples and Divisors
1. Find the common divisors of the following pairs of numbers:
– 12 and 18
– 24 and 36
– 15 and 25
– 8 and 10
– 21 and 28
2. Determine whether the following statements are true or false:
– 30 is a multiple of 5 and a divisor of 60.
– 16 is a multiple of 4 and a divisor of 32.
– 20 is a multiple of 10 and a divisor of 40.
– 45 is a multiple of 15 and a divisor of 90.
– 35 is a multiple of 5 and a divisor of 70.
Worksheet 4: Word Problems
1. Jenny has 24 candies, and she wants to share them equally among her 4 friends. How many candies will each friend receive? (Find the divisors of 24.)
2. John is buying books, and he wants to buy a set of 6 books. If there are 48 books in total, how many sets of 6 books can John buy? (Find the multiples of 6.)
3. A farmer has 18 eggs. He wants to pack them into cartons, with each carton holding 6 eggs. How many cartons can the farmer fill, and will there be any eggs left over? (Find the divisors of 18.)
4. There are 5 students in a row, and they each have 10 pencils. How many pencils are there in total? (Find the multiples of 10.)
Solutions
Worksheet 1: Multiples
1. Find the first five multiples of the following numbers:
– 3: 3, 6, 9, 12, 15
– 7: 7, 14, 21, 28, 35
– 12: 12, 24, 36, 48, 60
– 9: 9, 18, 27, 36, 45
– 5: 5, 10, 15, 20, 25
2. Determine whether the following statements are true or false:
– 18 is a multiple of 6. (True, 18 = 6 x 3)
– 25 is a multiple of 3. (False)
– 14 is a multiple of 5. (False)
– 10 is a multiple of 2. (True, 10 = 2 x 5)
– 21 is a multiple of 7. (True, 21 = 7 x 3)
Worksheet 2: Divisors
1. List all the divisors of the following numbers:
– 24: 1, 2, 3, 4, 6, 8, 12, 24
– 15: 1, 3, 5, 15
– 36: 1, 2, 3, 4, 6, 9, 12, 18, 36
– 8: 1, 2, 4, 8
– 10: 1, 2, 5, 10
2. Determine whether the following statements are true or false:
– 4 is a divisor of 16. (True, 16 ÷ 4 = 4)
– 9 is a divisor of 27. (True, 27 ÷ 9 = 3)
– 6 is a divisor of 14. (False)
– 12 is a divisor of 48. (True, 48 ÷ 12 = 4)
– 7 is a divisor of 49. (True, 49 ÷ 7 = 7)
Worksheet 3: Multiples and Divisors
1. Find the common divisors of the following pairs of numbers:
– 12 and 18: Common divisors are 1, 2, 3, and 6.
– 24 and 36: Common divisors are 1, 2, 3, 4, 6, 8, 12, and 24.
– 15 and 25: Common divisor is 5.
– 8 and 10: Common divisor is 2.
– 21 and 28: Common divisor is 7.
2. Determine whether the following statements are true or false:
– 30 is a multiple of 5 and a divisor of 60. (True)
– 16 is a multiple of 4 and a divisor of 32. (True)
– 20 is a multiple of 10 and a divisor of 40. (True)
– 45 is a multiple of 15 and a divisor of 90. (True)
– 35 is a multiple of 5 and a divisor of 70. (True)
Worksheet 4: Word Problems
1. Jenny has 24 candies, and she wants to share them equally among her 4 friends. How many candies will each friend receive?
– Solution: Each friend will receive 24 ÷ 4 = 6 candies.
2. John is buying books, and he wants to buy a set of 6 books. If there are 48 books in total, how many sets of 6 books can John buy?
– Solution: John can buy 48 ÷ 6 = 8 sets of 6 books.
3. A farmer has 18 eggs. He wants to pack them into cartons, with each carton holding 6 eggs. How many cartons can the farmer fill, and will there be any eggs left over?
– Solution: The farmer can fill 18 ÷ 6 = 3 cartons. There will be no eggs left over.
4. There are 5 students in a row, and they each have 10 pencils. How many pencils are there in total?
– Solution: There are 5 students, and each has 10 pencils, so there are a total of 5 x 10 = 50 pencils.
Arithmetic course and exercises





Responses