How to Learn Common Multiples Fast - A Step-by-Step Guide

Common multiples are a fundamental concept in mathematics. They are used in a variety of applications, from finding the least common denominator of fractions to calculating the time required to complete a task. If you struggle with common multiples, don’t worry! This course will teach you a simple and fast way to learn this important concept.

What are Common Multiples?

Common multiples are multiples that two or more numbers share in common. In other words, common multiples are numbers that are multiples of each of the given numbers. To find common multiples, you can identify the multiples of each number and look for the numbers that appear in the lists of multiples for all the given numbers.

Let’s take an example to illustrate common multiples. Suppose you want to find the common multiples of 4 and 6:

Multiples of 4: 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, …

Multiples of 6: 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, …

The common multiples of 4 and 6 are the numbers that appear in both lists. In this case, the common multiples are 12, 24, 36, and so on. These are the numbers that can be evenly divided by both 4 and 6.

Common multiples are often used in various mathematical problems and concepts, including finding common denominators for fractions or solving problems related to LCM (Least Common Multiple).

What Is a Least Common Multiple?

The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all of the given integers. In other words, the LCM is the smallest number that can be expressed as a linear combination of the given integers with non-negative coefficients.

The LCM is a useful concept in many areas of mathematics, including arithmetic, algebra, and geometry. It is also used in other disciplines, such as computer science and cryptography.

Example: Find the LCM of 6, 10, and 15.

List the Multiples of Each Number:

Multiples of 6: 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, …

Multiples of 10: 10, 20, 30, 40, 50, 60, 70, 80, 90, 100, …

Multiples of 15: 15, 30, 45, 60, 75, 90, 105, 120, 135, 150, …

Look for the numbers that appear in all three lists of multiples. These are the common multiples.

Common Multiples of 6, 10, and 15: 30, 60, 90,…

The LCM (Least Common Multiple) is the smallest common multiple among these numbers. In this case, the smallest common multiple is 30.

So, the common multiples of 6, 10, and 15 are 30, 60, and so on. The LCM of 6, 10, and 15 is 30.

Common Multiples of Two or More Natural Numbers

A natural number is a common multiple of two integers a and b if and only if it is both a multiple of a and b.

Example: 30 = 10 × 3

30 = 5 × 6

30 is a common multiple of 10 and 6, or 10 and 5, or 3 and 5, etc.

– The product of two natural numbers is a common multiple of these two numbers.

Example: 15 = 5 × 3

15 is a common multiple of 5 and 3.

Set of Common Multiples (non-zero) of Two Natural Numbers

Let M(4) be the set of multiples of 4 and M(6) be the set of multiples of 6.

M(4) = 4, 8, 12, 16, 20, 24, 28, 32 , 36, 40, 44, 48, 52, 56, 60, 64, 68, 72 …

M(6) = 6, 12, 18, 24, 30, 36, 42 , 48, 54, 60, 66, 72 , 78, 84, 90, 96, 102, 108, …

Let A be the set of common multiples of 4 and 6.

A = 12 , 24, 36, 48, 60, 72 …..

Least Common Multiple (LCM)

The “least common multiple of a and b” is called the smallest non-zero number in the set of common multiples.

Example: 12 is the least common multiple of 4 and 6 according to the set A above.

Note: Let’s revisit set A, which is the set of non-zero common multiples of 4 and 6.

A = 12, 24, 36, 48, 60, 72 …

It can be observed that 12 is the LCM, and A is the set of multiples of 12.

In conclusion: The set of common multiples of two natural numbers is equal to the set of multiples of their LCM.

Finding the LCM of Two Natural Numbers

To find the LCM of two non-zero natural numbers:

1) Decompose these numbers into their prime factors.

2) Take the product of all factors, each taken once and with its highest exponent.

Example: Find the LCM of 24 and 84.

1) Decompose these numbers into their prime factors:

24 ÷ 2 = 12

12 ÷ 2 = 6

6 ÷ 2 = 3

3 ÷ 3 = 1

24 = 2³ × 3

84 ÷ 2 = 42

42 ÷ 2 = 21

21 ÷ 3 = 7

7 ÷ 7 = 1

84 = 2² × 3 × 7

2) Take the product of all factors, each taken once and with its highest exponent.

The LCM of 24 and 84 is: 2³ × 3 × 7 = 8 × 3 × 7 = 168

Note 1: The LCM of two prime numbers or two coprime numbers is equal to their product.

Examples: – The LCM of 13 and 29 is equal to: 13 × 29 = 377

– The LCM of 15 and 14 is equal to: 15 × 14 = 210

Note 2: If a number a is a multiple of another number b, then the LCM of a and b is equal to a.

Example: The LCM of 150 and 450 is equal to 450 because 450 is a multiple of 150.”

How to find common multiples of a number quickly

To find common multiples of a number, you can use either of the following methods:

Method 1: Listing multiples

This method is straightforward, but it can be time-consuming for large numbers. To find common multiples of a number using this method, simply list the multiples of the number until you find a number that is divisible by all of the other numbers.

Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, … Multiples of 4: 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, …

The first common multiple of 3 and 4 is 12.

Method 2: Prime factorization

This method is more efficient than the listing multiples method, but it requires some knowledge of prime factorization. To find common multiples of a number using this method, first prime factorize each number. Then, the least common multiple (LCM) of the numbers is the product of the highest powers of each prime factor that appears in any of the numbers.

Example: Find the LCM of 6, 10, and 15.

Solution:

Prime factorize each number:

6 = 2 * 3 10 = 2 * 5 15 = 3 * 5

The LCM of the three numbers is the product of the highest powers of each prime factor that appears in any of the numbers:

LCM(6, 10, 15) = 2^1 * 3^1 * 5^1 = 30

Therefore, the LCM of 6, 10, and 15 is 30.

Both of these methods can be used to find common multiples of any number, regardless of how many numbers you are trying to find common multiples for.

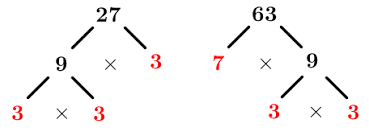
Least Common Multiple

Common multiples examples

Common multiples of 6 and 8

To find the common multiples of 6 and 8 using prime factorization, we first prime factorize each number:

Prime factors of 6 = 2 * 3
Prime factors of 8 = 2^3

The least common multiple (LCM) of 6 and 8 is the product of the highest powers of each prime factor that appears in any of the numbers. In this case, the LCM of 6 and 8 is the product of 2^3 * 3^1 = 24.

Therefore, 24 is the smallest number that is divisible by both 6 and 8.

The first few common multiples of 6 and 8:

24, 48 , 72,96, 120……

Common multiples of 10 and 12

List the Multiples of Each Number:

– Multiples of 10: 10, 20, 30, 40, 50, 60, 70, 80, 90, 100, …
– Multiples of 12: 12, 24, 36, 48, 60, 72, 84, 96, 108, …

Identify Common Multiples:

Now, compare the two lists and find the numbers that appear in both lists. These are the common multiples.

– The common multiples of 10 and 12 are 60 and any subsequent multiples like 120, 180, 240, etc.

So, the common multiples of 10 and 12 are 60, 120, 180, 240, and so on.

Common multiples of 8 and 12

List the Multiples of 8:
– Multiples of 8: 8, 16, 24, 32, 40, 48, 56, 64, 72, 80, 88, …

List the Multiples of 12:
– Multiples of 12: 12, 24, 36, 48, 60, 72, 84, 96, 108, …

Identify Common Multiples:
– Now, compare the lists of multiples and identify the numbers that appear in both lists.

The common multiples of 8 and 12 are: 24, 48, 72, …

Common multiples of 3 and 4

Start by listing the multiples of each number individually:

– Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, …
– Multiples of 4: 4, 8, 12, 16, 20, 24, 28, 32, …

Compare the lists of multiples and identify the numbers that appear in both lists. These are the common multiples:

– The common multiples of 3 and 4 are 12, 24, 36, 48, 60, 72, …

Common multiples of 3 and 5

List the Multiples of 3 and 5:

– Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, …
– Multiples of 5: 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, …

Identify Common Multiples:

Look at the lists of multiples for both 3 and 5 and identify the numbers that appear in both lists. These are the common multiples.

-The common multiples of 3 and 5 are: 15, 30, 45, …

Common multiples of 12 and 18

We can also use the prime factorization of each number to find the least common multiple (LCM). The LCM is the smallest number that is divisible by both numbers.

The prime factorization of 12 is 2^2 * 3, and the prime factorization of 18 is 2 * 3^2. The LCM of 12 and 18 is 2^2 * 3^2 = 36.

Therefore, the first three common multiples of 12 and 18 are 36, 72, and 108.

Common multiples of 6 and 9

List the Multiples of Each Number:

– Multiples of 6: 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, …
– Multiples of 9: 9, 18, 27, 36, 45, 54, 63, 72, 81, 90, …

Compare the lists of multiples and identify the numbers that appear in both lists. These are the common multiples.

– The common multiples of 6 and 9 are 18, 36, 54, …

How to Master the Art of Learning Common Multiples Fast

Common multiples are a fundamental concept in mathematics, and the ability to find them quickly and efficiently is essential for many mathematical operations. There are a few key strategies that can help you to master the art of learning common multiples fast.

1. Understand the concept of common multiples.

A common multiple of two or more numbers is a number that is divisible by all of the given numbers. For example, 12 is a common multiple of 2, 3, and 4, because 12 is divisible by 2, 3, and 4.

2. Memorize the common multiples of small numbers.

This will save you time when trying to find the common multiples of larger numbers. For example, the common multiples of 2 are 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, …

3. Use the prime factorization method.

For example, the prime factorization of 6 is 2 * 3, the prime factorization of 10 is 2 * 5, and the prime factorization of 15 is 3 * 5. The LCM of 6, 10, and 15 is the product of the highest powers of 2 and 3 that appear in any of the numbers, which is 2^1 * 3^1 * 5^1 = 30.

4. Practice regularly.

The more you practice, the faster you will become at finding common multiples.

5. Use visual aids.

Visual aids, such as number lines and Venn diagrams, can help you to understand the concept of common multiples and to find them more easily.

6. Play games.

There are many games and puzzles that can help you to learn common multiples in a fun and engaging way.

By following these strategies, you can master the art of learning common multiples fast and easily.

Here are some additional tips for learning common multiples fast in a professional setting:

Use a calculator or computer to help you prime factorize numbers. This will save you time and effort.
Create a spreadsheet or table to track the common multiples of frequently used numbers. This can be a valuable resource for quick reference.
Develop your own set of heuristics and shortcuts. This will help you to find common multiples even faster.

By mastering the art of learning common multiples fast, you can improve your efficiency and productivity in a variety of professional settings.