Worksheet on Understanding Matrices

Solve the following questions related to understand matrices. Refer to your knowledge and understanding of matrix basics, operations and properties.

Worksheets on Understanding Matrices

Matrix Basics

1. What is a matrix? What are its components?

2.What are the different types of matrices?

3. What are the different operations that can be performed on matrices?

4. What is the difference between a row matrix and a column matrix?

Matrix Notation

Write the notation for the following matrices:

a) A 2×3 matrix

b) A 3×2 matrix

c) A square matrix

Matrix Operations

1. Given matrices A and B:
A =

| 2 5 |
| 1 3 |

B =

| 4 2 |
| 7 0 |

Calculate the result of A + B.

2.Using matrices A and B from the previous question, calculate the result of A – B.

3. Matrix multiplication isn’t commutative. Explain this statement with an example.

Matrix Properties

1. State the conditions that two matrices must satisfy for matrix multiplication to be defined.

2.Describe the associative property of matrix multiplication. Provide an example to illustrate.

Applications of Matrices

1. In what fields are matrices commonly used? Provide two practical examples of how matrices are applied.

2.How are matrices used in computer graphics and 3D modeling?

Matrix Transformation

1. Explain how a matrix can be used to perform a scaling transformation on an object in a 2D space.

2. Describe a rotation matrix and its properties.

Answers

Matrix Basics

1. A matrix is a rectangular array of numbers, symbols, or expressions arranged in rows and columns. Its components are the individual entries within the matrix.

2.There are different types of matrices, including:

Square matrices

A square matrix has the same number of rows and columns.

Rectangular matrices

A rectangular matrix has different numbers of rows and columns.

Diagonal matrices

A diagonal matrix has all zero elements except for the elements on the main diagonal, which are all equal to a constant value.

Scalar matrices

A scalar matrix is a diagonal matrix with all elements on the main diagonal equal to the same number.

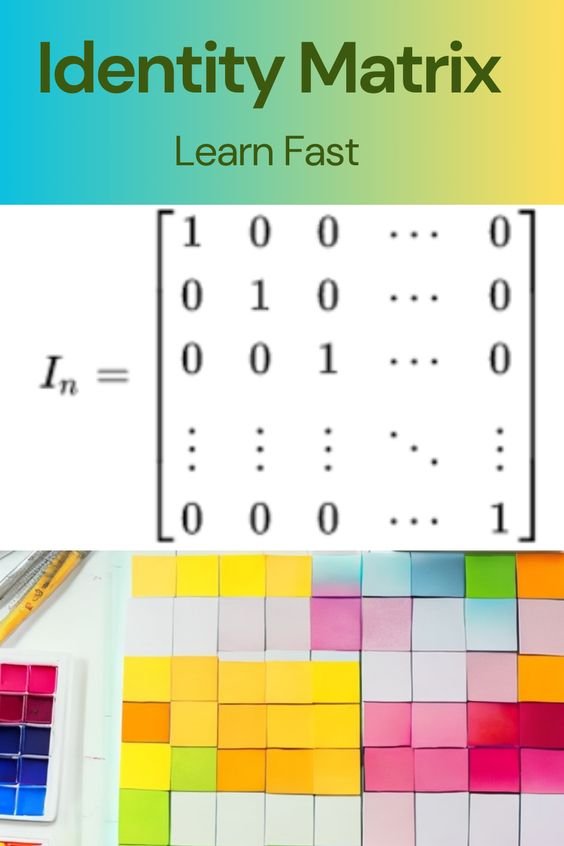
Identity matrices

An identity matrix is a square matrix with all elements on the main diagonal equal to 1 and all other elements equal to 0.

3.The following are some of the basic operations that can be performed on matrices:

Addition

Adding two matrices that have the same dimensions results in a matrix with the same dimensions.

Subtraction

Subtracting two matrices that have the same dimensions results in a matrix with the same dimensions.

Multiplication

Multiplying a matrix by a scalar results in a matrix with the same dimensions.

Matrix multiplication

Multiplying two matrices results in a matrix with the dimensions of the product of the two matrices.

Transpose

The transpose of a matrix is a matrix that has the rows and columns exchanged.

4. A row matrix has a single row and multiple columns, while a column matrix has a single column and multiple rows.

Matrix Notation

a) A 2×3 matrix is represented as [2 rows x 3 columns]

b) A 3×2 matrix is represented as [3 rows x 2 columns]

c) A square matrix is a matrix where the number of rows is equal to the number of columns.

Matrix Operations

1. A + B =
| 2+4 5+2 |
| 1+7 3+0 | =

| 6 7 |
| 8 3 |

2. A – B =

| 2-4 5-2 |
| 1-7 3-0 | =

| -2 3 |
| -6 3 |

3. Matrix multiplication is not commutative because the order of matrices matters. For example, AB ≠ BA.

Matrix Properties

1. For matrix multiplication to be defined, the number of columns in the first matrix must be equal to the number of rows in the second matrix.

2.The associative property of matrix multiplication states that when multiplying three matrices A, B, and C, the order of multiplication doesn’t affect the result: (A * B) * C = A * (B * C).

Applications of Matrices

1.Matrices are commonly used in mathematics, physics, computer science, engineering, and economics. Examples:
– Physics: Matrices represent quantum states in physics.
– Economics: Matrices model economic systems for analysis.

2.Matrices are used in computer graphics and 3D modeling to transform and render images by applying transformations like translation, rotation, and scaling.

Matrix Transformation

1.A matrix can perform a scaling transformation by multiplying each coordinate of an object by a scaling factor along each axis.

2.A rotation matrix is used to rotate objects in a 2D or 3D space. It preserves distances and angles between points and is typically in the form of a square matrix.

Worksheet on understanding Matrices with art

Objective:

To understand the concept of matrices and how they can be used to represent images.
To apply matrices to create art in a professional manner.

Instructions:

Read the introduction to matrices and how they can be used to represent images.
Complete the practice problems to solidify your understanding of matrices.
Create your own piece of art using matrices and submit it for evaluation.

Introduction:

A matrix is a rectangular arrangement of numbers into rows and columns. Matrices can be used to represent images by assigning each pixel in an image to a number in the matrix. For example, a black pixel could be represented by the number 0, and a white pixel could be represented by the number 1.

Practice Problems:

Create a matrix that represents a 3×3 image with all black pixels.
Create a matrix that represents a 4×4 image with a checkerboard pattern.
Create a matrix that represents a 5×5 image with a spiral pattern.

Creating Your Own Art:

Use your creativity to create your own piece of art using matrices. You can use any shapes, colors, or patterns that you want. Here are a few ideas to get you started:

Create a portrait of yourself or someone else.
Create a landscape of a place that you love.
Create a still life of objects in your home.
Create a abstract piece of art using random shapes and colors.

Evaluation:

Your work will be evaluated on the following criteria:

Accuracy: Your matrices should accurately represent the images that you are trying to create.
Creativity: Your work should be creative and original.
Neatness: Your work should be neat and organized.
Professionalism: Your work should be presented in a professional manner, including clear instructions and labeled figures.

Extension:

Research other ways to use matrices in art.
Create a piece of art that uses matrices to represent a moving image, such as a video or a GIF.
Write a blog post about your experience using matrices in art.

This worksheet helps you to understand matrices and how they can be used to create art in a professional manner. Have fun!

From Worksheet on Understanding Matrix to Learn Matrix Fast PAGE

From Worksheet on Understanding Matrix to HOME PAGE