Square Matrix – Definition,Examples,Fun Activities & Worksheets

When a matrix has both its rows and columns equal to ‘n’ in a square configuration, it is referred to as a square matrix of order ‘n’ or an ‘n-square’ matrix.
What is a Square Matrix?
A square matrix is a matrix that has the same number of rows and columns. For example, the following is a 3×3 square matrix:
[1 2 3]
[4 5 6]
[7 8 9]
The number of rows and columns in a square matrix is called its order. The order of the matrix above is 3.
The Principal Diagonal
The principal diagonal of a square matrix is the diagonal that runs from the top left corner of the matrix to the bottom right corner. The elements on the principal diagonal are called the diagonal elements of the matrix.
In the matrix above, the principal diagonal is 1, 5, and 9.
The Trace of a Square Matrix
The trace of a square matrix is the sum of the diagonal elements. In the matrix above, the trace is 1 + 5 + 9 = 15.
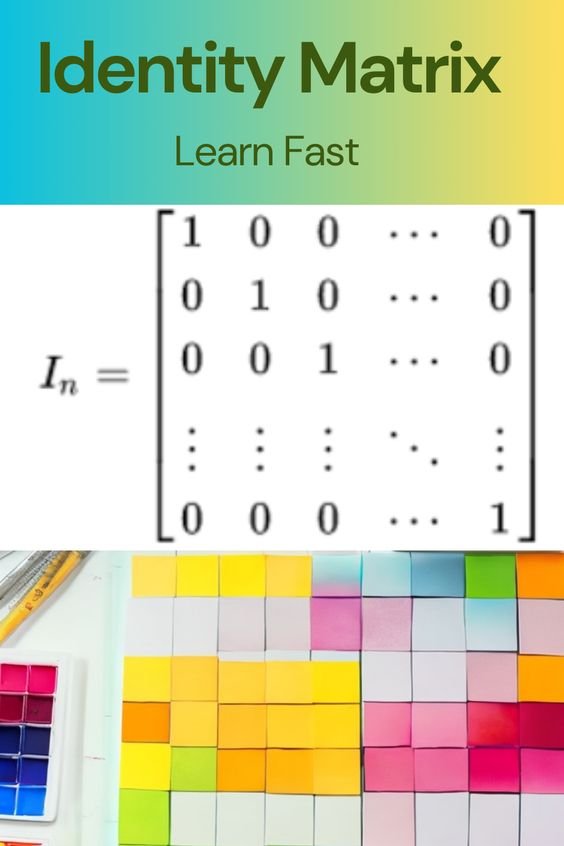
The Identity Matrix
An identity matrix is a square matrix with 1s on the principal diagonal and 0s everywhere else. The identity matrix of order n is denoted by In.
Here is the identity matrix of order 3:
[1 0 0]
[0 1 0]
[0 0 1]
Square Matrices in Linear Algebra
Square matrices are used in many different areas of mathematics, including linear algebra. Linear algebra is a branch of mathematics that deals with vectors and matrices. Square matrices are particularly important in linear algebra because they can be used to represent linear transformations.
A linear transformation is a function that takes a vector and maps it to another vector. Square matrices can be used to represent linear transformations because they can be used to multiply vectors.
For example, the following matrix can be used to represent a linear transformation that rotates a vector by 90 degrees counterclockwise:
[0 -1]
[1 0]
If we multiply this matrix by a vector, the vector will be rotated by 90 degrees counterclockwise.
Consider some examples
1.
| 3 7 |
| 1 5 |
The principal diagonal includes the elements 3 ,5.The diagonal elements are 3 ,5.
2.
| 5 9 2 |
| 7 1 8 |
| 6 4 3 |
The principal diagonal consists of the elements 5, 1, 3.Diagonal elements are 5, 1, 3.
3.
| 2 0 0 0 |
| 0 3 0 0 |
| 0 0 6 0 |
| 0 0 0 9 |
The principal diagonal elements are 2, 3, 6, 9.
Diagonal elements are 2, 3,6, 9.
4.
| 1 0 0 0 0 |
| 0 4 0 0 0 |
| 0 0 7 0 0 |
| 0 0 0 2 0 |
| 0 0 0 0 5 |
The principal diagonal elements are 1, 4, 7, 2, 5.Diagonal elements are 1, 4, 7, 2, 5.
Understanding the principal diagonal and diagonal elements is crucial when working with square matrices, as they often have special mathematical properties and applications in various fields of mathematics and beyond.
Interesting facts and stories about square matrices
The first mathematician to study square matrices was Leonhard Euler in the 18th century. He used them to solve systems of linear equations.
In the 19th century, Arthur Cayley developed the theory of determinants, which is a way of calculating the area of a square matrix. Determinants are used in many areas of mathematics, including linear algebra, differential equations, and geometry.
In the 20th century, John von Neumann developed the theory of linear operators, which is a way of studying square matrices that act on vectors. Linear operators are used in many areas of mathematics, including quantum mechanics, numerical analysis, and signal processing.
Square matrices are also used in computer graphics to represent the transformation of objects in 3D space. For example, a square matrix can be used to rotate an object, scale an object, or translate an object.
Square matrices are also used in cryptography to encrypt and decrypt messages. For example, the Rivest-Shamir-Adleman (RSA) algorithm uses square matrices to encrypt messages.
Gauss
Gauss was the first mathematician to prove that the determinant of a square matrix can be computed using only the elements of the matrix. He also developed the Gaussian elimination method for solving systems of linear equations.
Jacobi
Jacobi is considered one of the founders of linear algebra, and he made significant contributions to the theory of square matrices. Jacobi developed the Jacobi method for solving systems of linear equations, and he also proved the fundamental theorem of matrix algebra, which states that every square matrix can be decomposed into a product of a diagonal matrix and an orthogonal matrix.
George David Birkhoff
George David Birkhoff, an American mathematician, contributed to the study of square matrices and their transformations. He developed the Birkhoff–von Neumann theorem, which states that any doubly stochastic matrix (a square matrix with non-negative entries and whose rows and columns sum to 1) can be expressed as a convex combination of permutation matrices. This result has applications in fields like operations research, economics, and optimization.
Sylvester’s Determinant Theorem
James Joseph Sylvester, a British mathematician in the 19th century, made important contributions to the theory of matrices. He introduced the concept of the determinant and established Sylvester’s Determinant Theorem, which is a theorem about the determinants of products of square matrices. This theorem has practical applications in various fields, including physics, engineering, and computer science. It demonstrates the intricate relationships between the determinants of matrices and their products.
Cayley-Hamilton Theorem
The Cayley-Hamilton theorem, formulated by mathematicians Arthur Cayley and William Rowan Hamilton, is a fundamental result in linear algebra related to square matrices. The theorem states that every square matrix satisfies its own characteristic equation. This theorem provides insight into the behavior of matrices and has applications in areas like differential equations and control theory.
Eigenvalues and Eigenvectors
The study of eigenvalues and eigenvectors is central to square matrices. These concepts have profound implications in understanding the behavior of linear transformations and systems. They were extensively explored by mathematicians like Carl Friedrich Gauss and Peter Gustav Lejeune Dirichlet, contributing to various mathematical fields, including physics and engineering.
Square Matrices in the Real World
Square matrices are also used in many real-world applications, such as computer graphics, signal processing, and finance. In computer graphics, square matrices are used to represent 3D transformations, such as rotation, translation, and scaling. In signal processing, square matrices are used to filter signals. In finance, square matrices are used to calculate risk and return.
Square Matrices and the Human Body
Did you know that square matrices can be used to represent the human body? The human body can be divided into a grid of squares, and each square can be represented by a vector. The vectors can then be multiplied by a square matrix to represent the transformation of the body. This can be used to model things like muscle contraction, bone movement, and even the spread of disease.
Square Matrices and the Natural World
Square matrices can also be used to represent the natural world. For example, the weather can be modeled by a system of differential equations, which can be represented by square matrices. This can be used to predict things like the movement of storms and the amount of precipitation.
Square Matrices in Everyday Life
Square matrices are even used in everyday life! For example, when you use a calculator to multiply two numbers, the calculator is actually multiplying two matrices. And when you use a GPS to get directions, the GPS is using square matrices to calculate the shortest path between two points.
Fun and Educational Activities for Kids to Learn Square Matrix Fast
Matrices can seem like a daunting topic for kids, but they don’t have to be! With a little creativity, you can turn square matrices into a fun and educational activity for kids of all ages.
Multiplication Bingo
Make a bingo card with different matrices on it. Then, give kids a set of cards with numbers or letters on them. Have the kids roll a die or pick a number out of a hat to determine which matrix they need to multiply. If the matrix on their card matches the matrix on the bingo board, they get to mark it off. The first kid to get five in a row wins!

Matrices Maze
Create a maze out of different matrices. Then, give kids a set of cards with numbers or letters on them. Have the kids follow the maze by multiplying the numbers or letters they encounter. The first kid to reach the end of the maze wins!

Make a Multiplication Mural
This activity is a great way to help kids visualize how matrices are multiplied. Start by giving each child a square piece of paper. Then, have them draw a grid of dots on their paper, with the same number of rows and columns as the number of rows and columns in the matrix they are learning about. For example, if they are learning about a 2×2 matrix, they should draw a grid with 2 rows and 2 columns.
Once the kids have drawn their grids, have them label each dot with a number. The numbers can be anything they want, but it is helpful if they use consecutive numbers, starting from 1 in the top left corner and working their way down and across the grid.
Now, it’s time to multiply the matrices! Have the kids pair up and take turns multiplying their matrices together. To do this, they should line up the dots in their matrices so that the corresponding dots are in the same row and column. Then, they should multiply the numbers in each corresponding row and column together. The product of each row and column will be a new number that they should write in the corresponding row and column of their multiplication mural.
Continue multiplying matrices until the kids have filled up their murals. Once they are finished, they can take a step back and admire their work! This activity is a great way to help kids visualize how matrices are multiplied and to see how they can be used to represent different kinds of data.
Play a Matrices Game
There are many different matrices games that kids can play. One simple game is to have the kids roll two dice and then multiply the numbers together. The product of the dice roll will be the number of squares that the kid gets to color in on a square matrix. The kid with the most squares colored in at the end of the game wins!
Another fun matrices game is to have the kids play a scavenger hunt. Hide different objects around the house and then give each kid a matrix with a list of objects on it. The goal of the game is to find all of the objects on the list and then multiply the numbers together to find the total number of objects that were found. The kid who finds the most objects and has the highest total score wins!
These are just a few fun activities that can help kids learn about square matrices. With a little creativity, you can come up with many other activities that will make learning about matrices fun and engaging.
Start with small matrices. It can be helpful for kids to start with small matrices, such as 2×2 or 3×3 matrices. This will make it easier for them to visualize how the matrices work.
Use real-world examples. Whenever possible, try to use real-world examples to help kids understand matrices. For example, you could talk about how matrices are used to represent data in spreadsheets or to calculate the trajectory of a soccer ball.
Make it fun! Learning about matrices should be fun! Use games, puzzles, and other activities to make learning about matrices engaging and interactive.
Worksheets of Square Matrix
Square Matrix Operations
Matrix A:
| 3 7 |
| 2 5 |
Matrix B:
| 1 4 |
| 6 9 |
Questions:
- Calculate the sum of Matrix A and Matrix B.
- Multiply Matrix A by 2.
- Calculate the product of Matrix A and Matrix B.
- Find the transpose of Matrix B.
- Calculate the determinant of Matrix A.
Answers:
- Sum: | 4 11 | | 8 14 |
- Matrix A * 2: | 6 14 | | 4 10 |
- Product: | 45 65 | | 28 41 |
- Transpose of Matrix B: | 1 6 | | 4 9 |
- Determinant of Matrix A: 1
Square matrices are a powerful tool that can be used to represent linear transformations and solve many different kinds of problems. They are used in many different areas of mathematics and the real world. If you are interested in learning more about square matrices, I encourage you to take a linear algebra course.
Square Matrix Magic
Matrix C:
| 9 2 |
| 7 6 |
Matrix D:
| 3 5 |
| 8 1 |
Questions:
- Swap the positions of the top left and bottom right elements in Matrix C.
- Create a new matrix by subtracting Matrix D from Matrix C.
- Calculate the sum of the main diagonal elements of Matrix D.
- Find the trace of Matrix C.
- Determine if Matrix C is symmetric.
Answers:
- Swapped Matrix C: | 6 2 | | 7 9 |
- Matrix C – Matrix D: | 6 -3 | | -1 5 |
- Sum of main diagonal elements of Matrix D: 4
- Trace of Matrix C: 15
- Matrix C is not symmetric.
From Square Matrix to Matrix Course PAGE
From Square Matrix to HOME PAGE





Responses