Affine function vs Linear function vs Constant Function - What’s the difference?

In mathematics, there are three types of functions that are commonly used: affine function, linear function and constant function. These functions are all related, but they have different properties.

Affine function

What is Affine function?

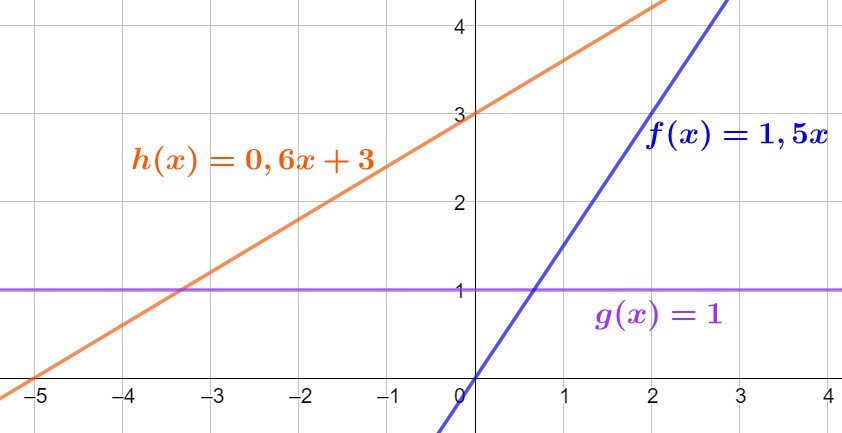
Affine functions are a type of mathematical function that is used to represent linear relationships between variables. An affine function is a function that can be expressed as the sum of a linear function and a constant term. In other words, an affine function is a function that can be written in the form f(x) = ax + b, where a and b are constants.

Example: f(x) = 30x+5 (a=30 and b=5)

Attention! There are more complex linear functions to identify!

f1(x) = 30x-5 (a=30 and b=-5)
f2(x) = 5+30x (a=30 and b=5)
f3(x) = x+5 (a=1 and b=5)
f4(x) = x/3+5 (a=1/3 and b=5)
f5(x) = -30x+5 (a=-30 and b=5)
f6(x) = -x+5 (a=-1 and b=5)

Affine function properties

Linearity

Affine functions are linear functions with an added constant term. This means that they represent straight lines when graphed, which have a constant slope.

General Form

The general form of an affine function is expressed as f(x) = ax + b, where:

f(x) is the output (dependent variable).

x is the input (independent variable).

a is the coefficient of the input variable, determining the slope of the line.

b is the constant term, determining the y-intercept, which is the point where the line intersects the y-axis.

Slope

The coefficient a represents the slope of the line. A positive a indicates an upward-sloping line, while a negative a represents a downward-sloping line. The magnitude of a determines the steepness of the slope.

Y-Intercept

The constant term b represents the y-intercept, which is the point where the line crosses the y-axis. It is the value of the function when x equals zero.

Linear Combination

Affine functions can be thought of as a combination of a linear transformation (the ax part) and a translation (the + b part). This makes them very versatile for modeling a wide range of real-world phenomena.

Parallel Lines

Affine functions with the same slope a are parallel to each other. Changing the value of b shifts the line up or down while keeping its slope constant.

Intersection

Two affine functions intersect when their graphs cross each other. The point of intersection represents the solution to a system of two affine equations.

Transformation

Affine functions are used extensively in linear algebra and geometry to describe transformations, such as translations, rotations, scaling, and shearing.

Affine Combinations

Linear combinations of affine functions, like af(x) + bg(x), where a and b are constants, also result in affine functions. This property is useful in various mathematical and engineering applications.

Affine Spaces

In mathematics, affine spaces are sets of points equipped with an affine structure defined by affine functions. These spaces play a fundamental role in various mathematical fields, including geometry and optimization.

Linear Functions

What is Linear Functions

A linear function is a particular type of affine function where b equals 0. Therefore, it is in the form of f(x) = ax.

Example: f(x) = 30x (a=30 and b=0)

Attention! Just like with classic affine functions, there are more complex linear functions to identify!

f(x) = x (a=1)
g(x) = x/5 (a=1/5)
h(x) = -2x (a=-2)
i(x) = -x (a=-1)

Linear Functions properties

Linear functions have several important properties that distinguish them from other types of functions.

Linearity

The most fundamental property of linear functions is that they are linear. This means that the relationship between the independent variable (usually denoted as x) and the dependent variable (usually denoted as f(x) or y) is a straight line. Mathematically, a function f(x) is linear if it can be expressed in the form f(x) = ax + b, where ‘a’ and ‘b’ are constants.

Slope

The slope of a linear function is a crucial property. It determines the steepness or incline of the line. In the equation f(x) = ax + b, ‘a’ represents the slope. A positive ‘a’ indicates an upward slope, a negative ‘a’ indicates a downward slope, and a zero ‘a’ represents a horizontal line.

Y-Intercept

Linear functions always intersect the y-axis at a specific point called the y-intercept. In the equation f(x) = ax + b, ‘b’ represents the y-intercept. It is the value of the function when x = 0, and it determines where the line crosses the y-axis.

Constant Rate of Change

Linear functions exhibit a constant rate of change. This means that for every unit increase in the independent variable ‘x’, the dependent variable ‘y’ changes by a fixed amount determined by the slope ‘a’. This constant rate of change is a defining characteristic of linear functions.

Parallel Lines

Linear functions with the same slope ‘a’ are parallel lines. They will never intersect, as long as they are not the same line. This property makes linear functions useful for solving problems involving parallel lines.

No Curvature

Linear functions do not exhibit curvature. Unlike quadratic or exponential functions, the graph of a linear function is a straight line with no bends or curves.

Proportional Relationships

Linear functions often represent proportional relationships. When ‘a’ is a constant multiple of ‘b’ (a = kb), the linear function represents direct proportionality. For example, if f(x) = 2x and g(x) = 3x, both functions represent direct proportionality between ‘x’ and ‘y’.

Infinite Domain and Range

Linear functions have an infinite domain and range. They extend indefinitely in both directions along the x-axis and y-axis, unless specified otherwise.

Linear Equations

Linear functions are often represented by linear equations. These equations are solvable in a straightforward manner, making linear functions essential in various fields, including physics, economics and engineering.

Affine function vs linear function – How do affine functions differ from linear functions?

Characteristic	Affine Function	Linear Function
General Form	f(x) = ax + b	f(x) = ax
Equation Structure	Combines both linear and constant terms	Contains only a linear term
Constants	Includes both ‘a’ and ‘b’ as constants	Includes only ‘a’ as a constant
Slope	The coefficient ‘a’ determines the slope	The coefficient ‘a’ determines the slope
Y-Intercept	The constant ‘b’ determines the y-intercept	There is no y-intercept (‘b’ is 0)
Linearity	Not restricted to passing through the origin	Always passes through the origin (0,0)
Geometric Representation	Represents a line with an arbitrary y-intercept	Represents a line passing through the origin

Affine Function:

An affine function combines both linear and constant terms.
It is represented in the form f(x) = ax + b, where ‘a’ and ‘b’ are constants.
‘a’ determines the slope of the line, while ‘b’ determines the y-intercept.
Affine functions are not restricted to passing through the origin (0,0) on a graph.
The graph of an affine function is a straight line with an arbitrary y-intercept.

Linear Function:

A linear function contains only a linear term.
It is represented in the form f(x) = ax, where ‘a’ is a constant.
‘a’ determines the slope of the line, but there is no separate constant for y-intercept.
Linear functions always pass through the origin (0,0) on a graph.
The graph of a linear function is a straight line that passes through the origin.

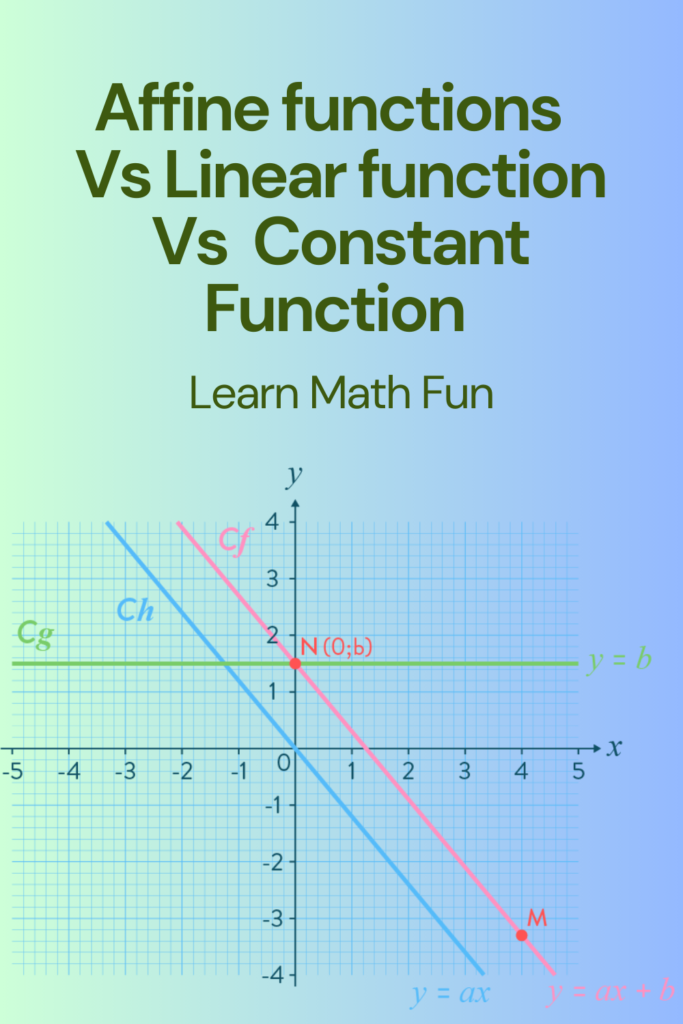
The main difference between affine and linear functions is that affine functions do not have to pass through the origin. This means that affine functions can be shifted up or down on the y-axis.

As you can see, the graphs of affine functions are simply shifted versions of the graphs of linear functions.

Constant Functions

What is constant function

A constant function is a function whose output value is the same for every input value. In other words, a constant function is a function whose graph is a horizontal line.

Constant functions are often used in mathematics to model real-world situations where a quantity remains constant. For example, the function f(x) = 98.6 degrees Fahrenheit is a constant function because the human body temperature remains relatively constant at 98.6 degrees Fahrenheit.

Constant function can also be used to represent constants in mathematical expressions. For example, the function f(x) = c is a constant function where c is a constant value.

Constant functions are relatively simple, but they can be useful in many different applications. For example, constant functions can be used:

In physics, to model the acceleration of a falling object due to gravity.
In economics, to model the price of a good or service that remains constant over time.
In computer science, to represent constants in programming languages.

Here are some examples of constant functions:

f(x) = 10
f(x) = 5
f(x) = 0
f(x) = π
f(x) = e

The graph of a constant function is a horizontal line. The y-intercept of the graph is the constant value of the function.

Attention! Some constant functions are also challenging to identify!

f(x) = -5 (b=-5)
g(x) = 1/3 (b=1/3)

There is also a form of affine function that is both linear and constant, where both a and b equal 0: f(x) = 0.

constant function graph

Why make a function constant?

Creating constant functions serves various mathematical and practical purposes. Here are why you might want to define or work with constant functions:

1. Mathematical Simplicity

Constant functions are the simplest type of functions. They are easy to work with and can serve as building blocks in more complex mathematical expressions. For example, in calculus or linear algebra, constant functions are often used to simplify equations.

2. Modeling Constant Quantities

In various mathematical and scientific models, there are situations where a quantity remains constant regardless of changes in other variables. For instance, the acceleration due to gravity near the surface of the Earth is approximately constant (9.81 m/s²). A constant function can represent such constants in equations.

3. Boundary Conditions

In certain mathematical problems, constant functions are used to define boundary conditions. For instance, when solving differential equations, constant functions can represent fixed or prescribed values at certain points in space or time.

4. Initial Values

In differential equations and dynamic systems, constant functions can represent initial conditions. These are the starting values of a variable before it evolves over time.

5. Simplifying Computations

In computer programming and numerical analysis, using constant functions can simplify code or algorithms. For example, when writing algorithms to process data, assigning a constant value can be a placeholder or a default value.

6. Constant Functions as Constants

Sometimes, constant functions are used to define constants or parameters in equations or algorithms. These constants can be easily adjusted to fine-tune the behavior of a system or model.

7. Teaching and Learning

In educational contexts, constant functions are often used to introduce fundamental concepts in mathematics and computer science. They provide a clear example of a basic mathematical concept.

Constant function properties

Constant functions have several distinct properties:

Constant Value

The most defining characteristic of a constant function is that it has a fixed, unchanging output value regardless of the input. In other words, for all x within the domain, f(x) is the same constant value. Mathematically, f(x) = c, where c is a constant.

Flat Line

When you graph a constant function, it appears as a horizontal line parallel to the x-axis. This line is at a constant height or y-value.

No Slope

Since the function is constant, it has zero slope. The rate of change is always zero because the output doesn’t change as the input varies.

Domain and Range

The domain of a constant function can be any set of real numbers because it doesn’t depend on the input. The range is a single value, the constant itself. So, the range is {c}, where c is the constant value.

Horizontal Asymptote

In calculus and limits, constant functions serve as horizontal asymptotes for other functions. For example, as x approaches infinity or negative infinity, the function approaches the constant value.

Additive and Multiplicative Identities

Constant functions are related to the additive and multiplicative identities in mathematics. If you add a constant function to any other function, it doesn’t change the shape of the other function. Similarly, if you multiply any function by a constant, it scales the function but retains its basic shape.

Use in Mathematics

Constant functions are essential in mathematics and physics for modeling quantities that do not change over time or with varying inputs. For example, the speed of light in a vacuum is a constant, often denoted by ‘c’ in physics equations.

Application

In real-world applications, constant functions can represent various scenarios, such as a fixed cost in economics, a constant voltage in electrical circuits, or a stable temperature in a controlled environment.

Simplicity

Constant functions are among the simplest functions in mathematics, making them useful for teaching fundamental concepts.

What’s the difference?

Linear functions are the simplest type of function. They are represented by a straight line on a graph. The slope of the line represents the rate of change of the function.

Affine functions are a generalization of linear functions. They are represented by a straight line on a graph, but they can be shifted up or down. This shift is represented by the constant term in the affine function equation.

Constant functions are the most specialized type of function. They have a constant value, regardless of the input value.

Type of function	Equation	Graph	Properties
Linear	y = mx	Straight line	Slope represents rate of change
Affine	y = mx + b	Straight line, shifted up or down	Constant term represents shift in the y-axis
Constant	y = c	Horizontal line	Output value is always the same