Number sets - A Fun and Beginner Guide

Number sets are a fundamental concept in mathematics. They are used to classify numbers based on their properties.

What are the 6 examples of Number sets

Natural numbers

The natural numbers are the counting numbers, starting from 1. They are represented by the symbol $N$ .

N = 1; 2; 3; 4…

Whole numbers

The whole numbers are the natural numbers, plus zero. They are represented by the symbol $W$ .

$W$ = 0; 1; 2; 3; 4…

Integers: The integers are all the whole numbers, positive and negative. They are represented by the symbol $Z$ .

$Z$ = …… -3; -2; -1; 0; 1; 2; 3…

Rational numbers: The rational numbers are all the numbers that can be expressed as a fraction of two integers. They are represented by the symbol $Q$ .

1/3 ∈ Q; 5 ∈ Q; -3.18 ∈ Q

Real numbers

The real numbers are all the numbers that can be represented on a number line. They are represented by the symbol $R$ .

π or √2; 0; -5; 0.67; 1/3; √3, and π belong to R.

Complex numbers

The complex numbers are all the numbers that can be expressed in the form $a + bi$ , where $a$ and $b$ are real numbers and $i$ is the imaginary unit. They are represented by the symbol $C$ .

Number set	Symbol	Definition
Natural numbers	$N$	The counting numbers, starting from 1.
Whole numbers	$W$	The natural numbers, plus zero.
Integers	$Z$	All the whole numbers, positive and negative.
Rational numbers	$Q$	All the numbers that can be expressed as a fraction of two integers.
Real numbers	$R$	All the numbers that can be represented on a number line.
Complex numbers	$C$	All the numbers that can be expressed in the form $a + bi$ , where $a$ and $b$ are real numbers and $i$ is the imaginary unit.

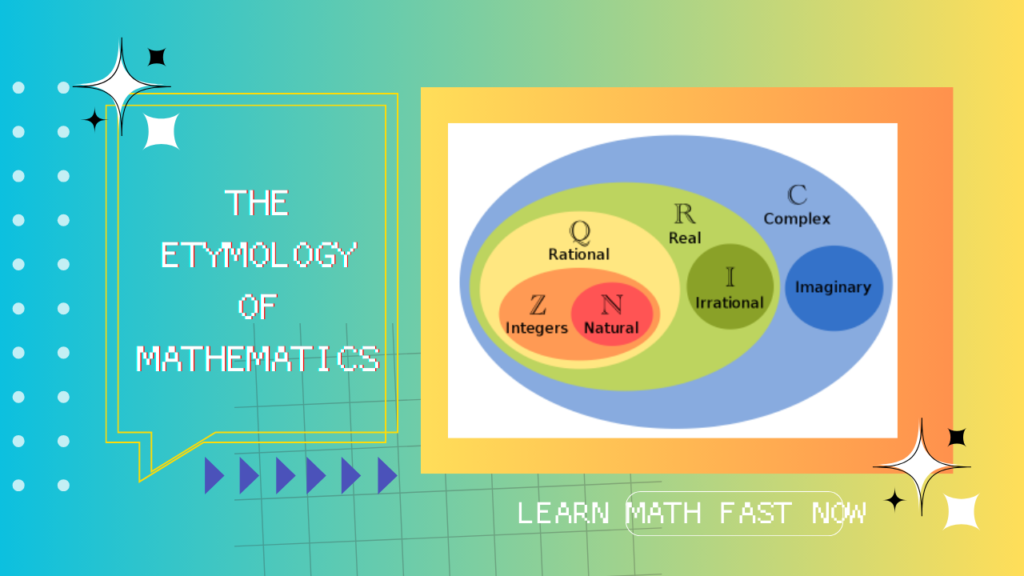
Natural Numbers (N) ⊂ Whole Numbers (W) ⊂ Integers (Z) ⊂ Rational Numbers (Q) ⊂ Real Numbers (R) ⊂ Complex Numbers (C)

This hierarchy represents how these sets are related to each other in mathematics.

Number sets in the real world

Number sets have practical applications in various real-world contexts. Here are some examples of how these number sets are used outside of pure mathematics:

Natural Numbers :
Counting: Natural numbers are used for counting objects in everyday life. For example, counting people, items on a shopping list, or days on a calendar.

Integers :
Temperature: Integers are used to represent temperatures in Celsius or Fahrenheit. Positive integers for temperatures above freezing and negative integers for temperatures below freezing.

Decimals :
Currency: Decimal numbers are used for representing currency values. For instance, prices in stores or financial transactions involve decimal numbers.

Rational Numbers :
Cooking: Recipes often involve fractions and ratios, which are rational numbers. For example, a recipe might call for 1/2 cup of flour.

Real Numbers :
Geometry: Real numbers are used extensively in geometry to represent lengths, areas, and volumes. For instance, the length of a side of a square or the volume of a sphere is represented using real numbers.
Physics: Real numbers are used in physics to describe physical quantities such as speed, distance, and time.
Economics: Real numbers are used in economic models to represent variables like GDP, inflation rates, and interest rates.
Engineering: Engineers use real numbers in various calculations, including stress analysis, structural design, and electrical circuit analysis.

In essence, number sets are fundamental to describing and understanding various aspects of the real world, from everyday activities to complex scientific and economic analyses. They provide a common language for quantifying and communicating quantities and measurements across different fields and disciplines.

Fun activities with number sets

Here are some fun activities that you can do to learn more about number sets:

Play number set games. There are many different games that you can play to learn about number sets. For example, you can play a game where you have to sort numbers into different sets, or a game where you have to answer questions about the properties of different number sets.
Create number set puzzles. You can create your own number set puzzles by writing down numbers on different pieces of paper and then asking someone to sort them into the correct sets.
Use number sets in everyday life. Look for ways to use number sets in your everyday life. For example, you can use natural numbers to count the number of steps you take in a day, or you can use whole numbers to represent the amount of money you have in your pocket.

By learning about number sets and using them in fun and creative ways, you can develop a deeper understanding of this important mathematical concept.

Worksheets

Worksheet 1: Natural Numbers (N)

Question 1: Write the first five natural numbers.

Answer 1: 1, 2, 3, 4, 5

Question 2: What is the 10th natural number?

Answer 2: 10

Question 3: Is zero a natural number? (Yes/No)

Answer 3: No

Worksheet 2: Whole Numbers (W)

Question 1: Write the first three whole numbers.

Answer 1: 0, 1, 2

Question 2: What is the successor of 7 in whole numbers?

Answer 2: 8

Question 3: List two whole numbers less than -1.

Answer 3: -2, -3

Worksheet 3: Integers (Z)

Question 1: Name three positive integers.

Answer 1: 1, 2, 3

Question 2: Give the opposite of -5.

Answer 2: 5

Question 3: Write down an integer that is neither positive nor negative.

Answer 3: 0

Worksheet 4: Rational Numbers (Q)

Question 1: Express 2/3 as a rational number.

Answer 1: 2/3

Question 2: Is 5 an irrational number? (Yes/No)

Answer 2: No

Question 3: Add -1/4 and 3/4.

Answer 3: 2/4 (or 1/2)

Worksheet 5: Real Numbers (R)

Question 1: Plot the point on a number line that represents the number √2.

Answer 1: (Approximately 1.41 on the number line)

Question 2: Is π a real number? (Yes/No)

Answer 2: Yes

Question 3: Give an example of a real number that is not rational.

Answer 3: √3

Worksheet 6: Complex Numbers (C)

Question 1: Express 3 + 2i in the standard form a+bi.

Answer 1: 3 + 2i

Question 2: Find the real and imaginary parts of the complex number 4 – 7i.

Answer 2: Real part: 4, Imaginary part: -7

Question 3: Add (1 + 2i) and (3 – 5i).

Answer 3: 4 – 3i

Question 4: Subtract (2 – i) from (6 + 3i).

Answer 4: 4 + 4i

Question 5: Multiply (2 + 3i) by (1 – 4i).

Answer 5: 14 – 5i

Question 6: Calculate the absolute value (modulus) of the complex number 5 + 12i.

Answer 6: √(5^2 + 12^2) = √(25 + 144) = √169 = 13

Question 7: Find the complex conjugate of 2 – 8i.

Answer 7: 2 + 8i

Question 8: Divide (6 – 3i) by (2 + i).

Answer 8: (6 – 3i) / (2 + i) = (6 – 3i)(2 – i) / (2^2 + 1^2) = (12 – 6i – 3i + 3i^2) / 5 = (12 – 9i – 3) / 5 = (9 – 9i) / 5

Question 9: Find a complex number whose square is -16.

Answer 9: ±4i (since (4i)^2 = -16 and (-4i)^2 = -16)

Question 10: Write down a complex number that is neither purely real nor purely imaginary.

Answer 10: Any complex number with both real and imaginary parts, e.g., 3 + 2i.

Worksheet 7: are these number sets the same 1267343 1276343

1267343:

This is a natural number because it is a positive whole number.

It belongs to the set N (natural numbers).

1276343:

This is also a natural number because it is a positive whole number.

It also belongs to the set N (natural numbers).

So, both of these numbers fall into the same set, which is the set of natural numbers (N). However, they are not the same number; they have different numerical values.

Number sets to Arithmetic course and exercises