Rational Numbers - Definition ,Applications,Worksheets & Fun activities

Rational numbers are a type of number that can be expressed as a fraction of two integers, where the denominator is not zero. For example, 1/2, 2/3, and 5/7 are all rational numbers.

Rational numbers are important because they can be used to represent many different types of quantities, such as fractions, decimals, and percentages. They are also used in many different areas of mathematics, such as algebra, geometry, and calculus.

What are Rational Numbers?

In mathematics,a rational number is a numerical value that can be precisely represented as a quotient or fraction, adhering to the structure p/q. Here, ‘p’ stands for the numerator, ‘q’ represents the non-zero denominator, and the ratio p/q is expressed in its simplest form, where ‘p’ and ‘q’ share no common factors.

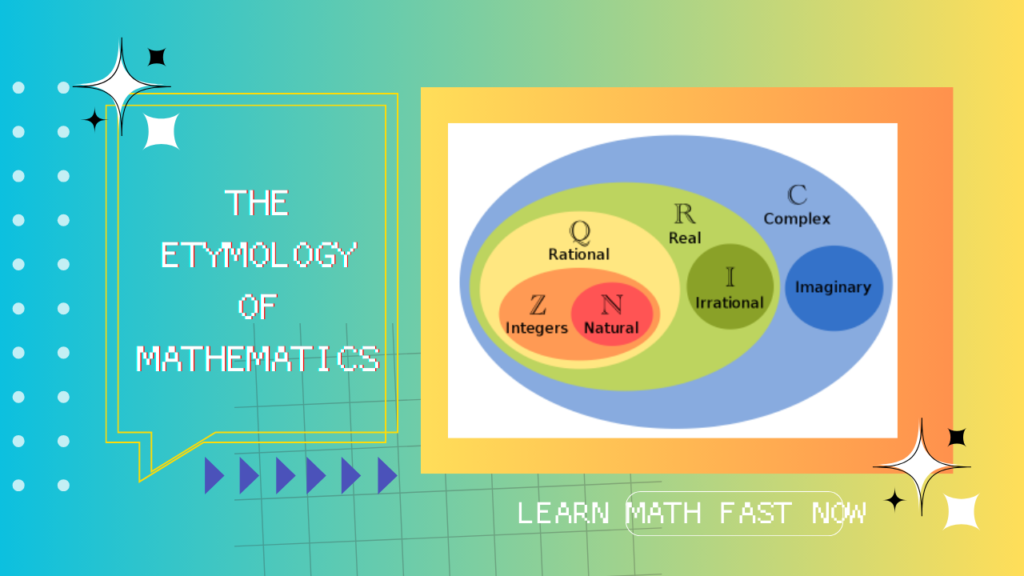
Moreover, the family of rational numbers ( Q) resides within the broader expanse of real numbers. Delving deeper, rational numbers encompass integers (Z) within their domain, which, in turn, encompass natural numbers (N). Therefore, both integers and fractions harmoniously find their representation within this structured p/q format. This inclusive nature allows us to categorize all integers and fractions as rational numbers.

In the elegant form of p/q, ‘q’ holds the flexibility to take on any numeric value. In fact, ‘q’ is not restricted from being equal to 1. A fascinating outcome arises when ‘q’ takes on this value; it leads to every integer emerging as a rational number. The complete ensemble of rational numbers is symbolically captured by the notation ‘Q’.

Note: N ⊂ W ⊂ Z ⊂ Q

Rational numbers can also be expressed as decimals. For example, 0.5, 0.33333, and 1.25 are all rational numbers. In fact, any decimal number that terminates (has a finite number of digits after the decimal point) or repeats (has a pattern of digits that repeats forever) is a rational number.

How to Identify Rational Numbers

There are a few different ways to identify rational numbers. One way is to look for numbers that can be expressed as a fraction of two integers. For example, 1/2, 2/3, and 5/7 are all rational numbers because they can be expressed as a fraction of two integers.

Another way to identify rational numbers is to look for numbers that can be expressed as a decimal with a finite number of digits after the decimal point. For example, 0.5, 0.33333, and 1.25 are all rational numbers because they can be expressed as decimals with a finite number of digits after the decimal point.

Finally, rational numbers can also be identified by looking for numbers that can be expressed as a percentage. For example, 50%, 33.33%, and 125% are all rational numbers because they can be expressed as percentages.

Properties of Rational Numbers

Rational numbers have a number of properties that make them useful in mathematics. Some of these properties include:

Rational numbers can be added, subtracted, multiplied, and divided.
The sum, difference, product, and quotient of two rational numbers is always a rational number.
Rational numbers can be ordered. For example, 1/2 is less than 3/4.
Rational numbers can be represented on a number line.

Applications of Rational Numbers

Rational numbers are used in many different areas of mathematics, such as algebra, geometry, and calculus. They are also used in many different fields, such as science, engineering, and finance.

Here are a few examples of how rational numbers are used in different areas:

Area	Application of Rational Numbers	Arithmetical Operation Examples
Algebra	Solving equations and inequalities	Solve for x: 3x + 5 = 11
Geometry	Measuring lengths, areas, and volumes	Find the area of a rectangle with sides 3/4 and 1/2 units
Calculus	Finding limits, derivatives, and integrals	Calculate the derivative of f(x) = (2x^2 + 3x + 1) / (x + 2)
Science	Modeling physical quantities (e.g., speed, acceleration, force)	Calculate acceleration: a = (v_f – v_i) / t
Engineering	Designing structures, machines, and systems	Determine gear ratio: Gear 1 has 24 teeth, Gear 2 has 36 teeth
Finance	Calculating interest rates, dividends, and profits	Compute compound interest: A = P(1 + r/n)^(nt)

Algebra

Rational numbers are used to solve equations and inequalities, such as:

- $2 x + 3 = 5$ , which can be solved by subtracting 3 from both sides and dividing both sides by 2 to get $x = 1$ .
- $x > 3$ , which can be solved by adding 3 to both sides to get $x = 3 + 3 = 6$ .

Geometry

Rational numbers are used to measure lengths, areas, and volumes, such as:

- The length of a line segment can be calculated by dividing the distance between two points by the number of segments it takes to cover the distance. For example, the length of a line segment with endpoints (0, 0) and (1, 1) can be calculated by dividing the distance between the two points (1) by the number of segments it takes to cover the distance (2), which is $2 1$ .
- The area of a rectangle can be calculated by multiplying the length of the base by the height. For example, the area of a rectangle with base 2 and height 3 can be calculated by multiplying 2 by 3, which is 6.
- The volume of a box can be calculated by multiplying the length, width, and height. For example, the volume of a box with length 2, width 3, and height 4 can be calculated by multiplying 2 by 3 by 4, which is 24.

Calculus

Rational numbers are used to find limits, derivatives, and integrals, such as:

- The limit of a function as $x$ approaches a certain value can be calculated by letting $x$ approach the value and seeing what the value of the function approaches. For example, the limit of the function $f (x) = x + 1 x$ as $x$ approaches 1 is 1.
- The derivative of a function can be calculated using the limit definition of the derivative. For example, the derivative of the function $f (x) = x^{2}$ is $2 x$ .
- The integral of a function can be calculated using the fundamental theorem of calculus. For example, the integral of the function $f (x) = x^{2}$ from 0 to 1 is $3 1$ .

Science

Rational numbers are used to model physical quantities, such as speed, acceleration, and force, such as:

- Speed: Speed is the rate of change of distance over time, and it can be expressed as a rational number, such as 10 miles per hour or 20 meters per second.
- Acceleration: Acceleration is the rate of change of speed over time, and it can be expressed as a rational number, such as 5 feet per second per second or 10 meters per second squared.
- Force: Force is the product of mass and acceleration, and it can be expressed as a rational number, such as 10 pounds or 20 newtons.

Engineering

Rational numbers are used to design structures, machines, and systems, such as:

- Designing a bridge: The strength of a bridge is determined by the materials used and the forces acting on it. These forces can be expressed as rational numbers, and they must be carefully balanced to ensure the safety of the bridge.
- Designing a machine: The efficiency of a machine is determined by the ratio of output power to input power. This ratio can be expressed as a rational number, and it must be as high as possible to ensure the efficiency of the machine.
- Designing a system: The complexity of a system is determined by the number of components and the interactions between them. These interactions can be expressed as rational numbers, and they must be carefully considered to ensure the reliability of the system.

Finance

Rational numbers are used to calculate interest rates, dividends, and profits, such as:

- Interest rate: The interest rate is the percentage of a loan that is paid back to the lender each year. It can be expressed as a rational number, such as 5% or 10%.
- Dividend: A dividend is a portion of a company’s profits that is paid to shareholders. It can be expressed as a rational number, such as $0.25 per share or $0.50 per share.
- Profit: Profit is the difference between a company’s revenue and expenses. It can be expressed as a rational number, such as $1 million or $2 million.

In each of these areas, rational numbers play a crucial role in performing arithmetical operations and solving various problems. Whether it’s manipulating equations in algebra, measuring dimensions in geometry, or optimizing designs in engineering, rational numbers provide a solid mathematical foundation for practical applications across multiple disciplines.

The Importance of Learning Rational Numbers

Rational numbers are an important part of mathematics, and they are used in many different areas of life. Learning about rational numbers can help students develop their mathematical skills and understanding. It can also help them to see the relevance of mathematics in the real world.

Rational numbers are also important for everyday life. For example, we use rational numbers to measure things like distance, weight, and time. We also use rational numbers to calculate things like interest, profit, and loss.

Learning about rational numbers can help students develop their critical thinking skills. When students learn how to identify and work with rational numbers, they learn how to think logically and solve problems. They also learn how to make sense of the world around them.

How are rational numbers used in art?

Rational numbers are used in art in a variety of ways. For example, they are used to measure the proportions of objects in a painting or sculpture. They are also used to create patterns, such as the Fibonacci sequence, which is a series of numbers where each number is the sum of the two previous numbers. The Fibonacci sequence can be found in nature, as well as in art, and it is often used to create beautiful and harmonious designs.

Rational numbers and the golden ratio

One of the most famous examples of rational numbers in art is the golden ratio. The golden ratio is a special number that is often found in nature and in art. It is approximately equal to 1.618. The golden ratio is often used to create designs that are aesthetically pleasing. For example, the Parthenon in Athens is said to have been designed using the golden ratio.

Fractals in art

Fractals are another example of how rational numbers are used in art. Fractals are patterns that are repeated infinitely. They can be found in nature, such as in snowflakes and fern leaves. Fractals can also be created using mathematical equations. Fractals are often used in art to create beautiful and complex designs.

How can you use rational numbers in your art?

There are many ways to use rational numbers in your art. You can use them to measure proportions, create patterns, or even incorporate the golden ratio or fractals into your designs. If you’re not sure how to get started, there are many resources available online and in libraries that can help you learn more about how to use rational numbers in art.

Here are a few ideas for how you can use rational numbers in your art:

Create a painting or sculpture using precise measurements.
Use the Fibonacci sequence to create a pattern in your art.
Incorporate the golden ratio into your design.
Create a fractal art piece.

No matter how you choose to use them, rational numbers can be a powerful tool for creating beautiful and unique art. So get creative and see what you can come up with!

Fun activities to learn rational numbers fast

Bellow are some of our favorite activities for learning about rational numbers. These activities are perfect for kids of all ages, and they are sure to make learning about rational numbers fun and engaging.

The Fraction Game

This is a great activity for kids who are just starting to learn about fractions. To play, you will need a deck of cards with fractions on them. You can make your own cards, or you can buy a set of fraction cards online or at a toy store.

To play, deal out the cards face down to each player. Each player should turn over their top card and place it in front of them. The player with the highest fraction wins the round.

If two players have the same fraction, they can play a tiebreaker round. In the tiebreaker round, each player will add their fraction to another fraction that they choose. The player with the highest sum wins the round.

The Rational Number Scavenger Hunt

This is a great activity for kids who are a little more familiar with rational numbers. To play, you will need to create a list of rational numbers. You can make your own list, or you can find a list online.

Once you have created your list, hide the rational numbers around your house or yard. Give the kids a list of the rational numbers they are looking for, and let them go on a scavenger hunt to find them.

The first kid to find all of the rational numbers wins the game.

The Rational Number Pizza Party

This is a great activity for kids who love pizza and math. To play, you will need to make a pizza with a variety of toppings. You will also need to cut the pizza into slices.

Before you cut the pizza, write a rational number on each slice. The rational numbers should be different from each other.

Once the pizza is cut, let the kids eat the pizza. As they eat, they should try to figure out the rational number on each slice.

The kid who correctly identifies the most rational numbers wins the game.

The Rational Number Relay Race

This is a great activity for kids who are up for a challenge. To play, you will need two teams of kids. Each team will need a set of fraction cards.

To start the race, the first kid on each team will flip over a card. The kid with the highest fraction will run to the finish line and back. The next kid on their team will then flip over a card, and the race will continue.

The first team to get all of their kids to the finish line wins the game.

The Rational Number Mad Libs

This is a great activity for kids who love to be creative. To play, you will need a set of rational number mad libs. You can make your own mad libs, or you can find a set online.

To play, give each kid a set of rational number mad libs. The kids will then fill in the blanks to create a story.

Once the kids have finished their stories, they can share them with each other.

In conclusion, rational numbers are an important part of mathematics and everyday life. Learning about rational numbers can help students develop their mathematical skills, critical thinking skills, and understanding of the world around them.

Worksheets Rational Numbers

Worksheet 1: Exploring Rational Numbers

Instructions: Solve the following problems involving rational numbers.

Calculate the following rational number additions:a) 1/3 + 2/5 b) 7/8 + 1/4 c) 5/6 + 3/6 d) 4/9 + 2/9
Evaluate the rational number subtractions:a) 3/4 – 1/4 b) 5/6 – 2/6 c) 7/9 – 1/9 d) 2/3 – 1/3
Simplify the rational number expressions:a) (12/18) ÷ (4/6) b) (15/20) × (5/3) c) (9/27) + (1/3) d) (10/25) – (2/5)
Compare the following rational numbers using >, <, or =:a) 2/5 ___ 3/5 b) 1/3 ___ 2/3 c) 4/7 ___ 5/7 d) 5/8 ___ 3/8
Convert the following fractions to decimals:a) 3/4 b) 2/5 c) 5/6 d) 7/8

Answers:

a) 11/15 b) 5/8 c) 1 d) 2/3
a) 1/2 b) 1/3 c) 2/3 d) 1/3
a) 1 b) 1 c) 1 d) 1
a) < b) < c) < d) >
a) 0.75 b) 0.4 c) 0.8333… d) 0.875

Worksheet 2: Real-life Applications of Rational Numbers

Instructions: Solve the following real-life problems involving rational numbers.

A recipe calls for 2/3 cup of flour. If you want to make half the recipe, how much flour do you need?
Maria spent 3/5 of her allowance on a book and 1/5 on a toy. What fraction of her allowance did she spend in total?
A swimming pool is 4/5 full. If 2/5 of the water is drained, what fraction of the pool’s capacity is now filled with water?
An art project requires 3/4 yard of ribbon. If Sarah has 2/3 yard of ribbon, how much more does she need to complete the project?

Answers:

1/3 cup
4/5
2/5
1/12 yard

These worksheets provide an interactive and engaging way for students to practice their understanding of rational numbers while also applying them to real-life scenarios.

From Rational Numbers to HOME PAGE

Rational Numbers – Definition ,Applications,Worksheets & Fun activities

What are Rational Numbers?

How to Identify Rational Numbers

Properties of Rational Numbers