Learn The Types of Matrices Fast- Classification,Examples,Fun activities & worksheets

We will discuss here about the types of matrices.
Matrices are classified according to the following:
- The number of rows and columns: A matrix with a single row is called a row matrix. A matrix with a single column is called a column matrix. A matrix with more than one row and more than one column is called a rectangular matrix.
- The specific elements they contain: A matrix with all zeros is called a zero matrix. A square matrix with ones on the leading diagonal and zeros elsewhere is called an identity matrix. A square matrix that is symmetric about its leading diagonal is called a symmetric matrix. A square matrix that is antisymmetric about its leading diagonal is called an antisymmetric matrix.
The types of matrices
Here are some of the most common types of matrices:
- Row matrix: A matrix with only one row is called a row matrix. A row matrix can be thought of as a vector, but it is more specifically a 1-dimensional array. For example, the following is a row matrix with 3 elements:
[1 2 3]
- Column matrix: A matrix with only one column is called a column matrix. A column matrix can be thought of as a vector, but it is more specifically a 1-dimensional array. For example, the following is a column matrix with 3 elements:
| 8 | | 9 | | 7 |
- Rectangular matrix: A matrix with more than one row and more than one column is called a rectangular matrix. A rectangular matrix can be thought of as a 2-dimensional array. For example, the following is a rectangular matrix with 2 rows and 3 columns:
[1 2 3]
[4 5 6]
- Square matrix: A matrix with the same number of rows and columns is called a square matrix. A square matrix can be thought of as a special type of rectangular matrix. For example, the following is a square matrix with 3 elements:
[1 2 3]
[2 4 6]
[3 6 9]
- Zero matrix: A matrix with all zeros is called a zero matrix. A zero matrix can be a row matrix, a column matrix, or a square matrix. For example, the following is a 3×3 zero matrix:
[0 0 0]
[0 0 0]
[0 0 0]
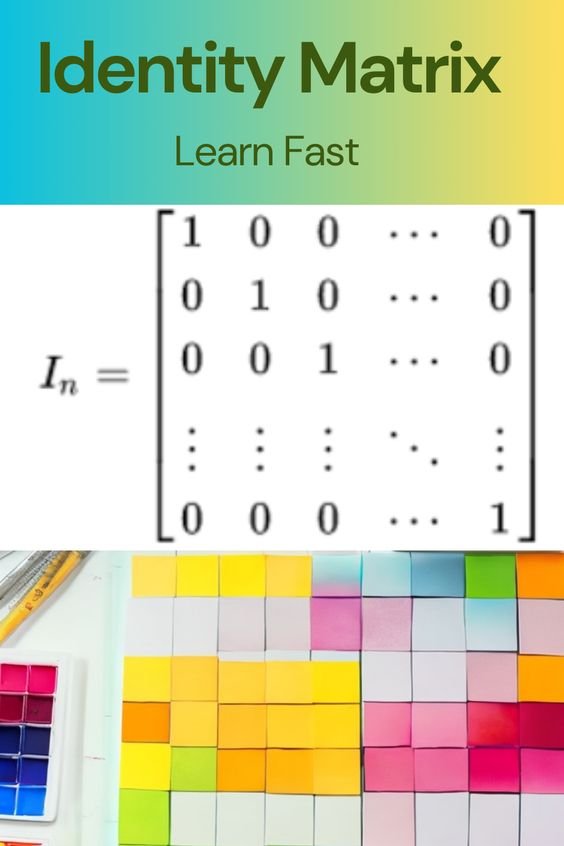
- Identity matrix: A square matrix with ones on the leading diagonal and zeros elsewhere is called an identity matrix. The identity matrix is a special type of square matrix that has many useful properties. For example, the following is a 3×3 identity matrix:
[1 0 0]
[0 1 0]
[0 0 1]
- Diagonal Matrix
A diagonal matrix is a square matrix where all of the elements below the main diagonal are zero. For example, the following is a 3×3 diagonal matrix:
[1 0 0]
[0 5 0]
[0 0 9]
- Upper Triangular Matrix
An upper triangular matrix is a square matrix where all of the elements below the main diagonal are zero. For example, the following is a 3×3 upper triangular matrix:
[1 2 3]
[0 5 6]
[0 0 9]
- Lower Triangular Matrix
A lower triangular matrix is a square matrix where all of the elements above the main diagonal are zero. For example, the following is a 3×3 lower triangular matrix:
[1 0 0]
[2 5 0]
[3 6 9]
- Symmetric Matrix
A symmetric matrix is a square matrix that is equal to its transpose. For example, the following is a 3×3 symmetric matrix:
[1 2 3]
[2 5 6]
[3 6 9]
- Antisymmetric Matrix
An antisymmetric matrix is a square matrix where the transpose of the matrix is equal to the negative of the matrix. For example, the following is a 3×3 antisymmetric matrix:
[0 1 2]
[-1 0 -3]
[-2 3 0]In addition to these common types of matrices, there are many other specialized types of matrices, such as diagonal matrices, triangular matrices, symmetric matrices, and skew-symmetric matrices. These matrices have specific properties that make them useful for different applications.
Fun activities to learn about the different types of matrices
We will share some more ideas for fun activities that can help students learn about the different types of matrices.If you have a lot of students, you can divide them into teams. The team with the most correct answers wins!
- Matrices Identification Game: This is a great activity for introducing students to the different types of matrices. You can create a set of cards with different types of matrices, such as square matrices, diagonal matrices, and identity matrices. Students can take turns identifying the type of matrix on each card. The student who correctly identifies the most matrices wins!
Use colorful cards and/or images to represent the different types of matrices.
Make the cards large enough so that students can easily read the information.
- Matrices Scavenger Hunt: This is a great activity for getting students up and moving around. You can create a list of different types of matrices and hide them around the classroom or school. Students can work in teams to find the matrices and identify their type. The team that finds the most matrices and correctly identifies their type wins!
Hide the matrices in different places around the classroom or school.
Make sure that the matrices are easy to find, but not too easy.
- Matrices Quiz Bowl: This is a great activity for testing students’ knowledge of the different types of matrices. You can create a quiz bowl with different categories and questions about matrices. Students can work in teams to answer the questions. The team with the most correct answers wins!
Make the questions challenging, but not too difficult.
Use a timer to add excitement to the game.
- Matrices Word Search: This is a great activity for students who enjoy word puzzles. You can create a word search with different types of matrices hidden in the puzzle. Students can work individually or in teams to find the matrices. The student or team who finds the most matrices first wins!
Use different colors and fonts to make the word search more visually appealing.
Make sure that the words are not too difficult to find.
- Matrices Puzzles: This is a great activity for students who enjoy problem-solving. You can create different types of puzzles that involve matrices. For example, you could create a jigsaw puzzle with different matrices pieces, or a crossword puzzle with matrix-related clues.
Make the puzzles challenging, but not too difficult.
Provide clear instructions for each puzzle.
Be prepared to answer questions that students may have.
Make sure that the puzzles are appropriate for the level of the students.
Fun worksheets
Bellow are some fun worksheets for types of matrices to learn types of matrices fast with answers:
Identify the type of matrix
In this worksheet, students will be given a matrix and asked to identify its type. There are four types of matrices: square, diagonal, identity, and triangular.
Questions:
- Identify the type of matrix:
[1, 2, 3]
[4, 5, 6]
[7, 8, 9]
- Identify the type of matrix:
[1, 0, 0]
[0, 2, 0]
[0, 0, 3]
- Identify the type of matrix:
[1, 0]
[0, 1]
- Identify the type of matrix:
[1, 2, 3]
[0, 4, 5]
[0, 0, 6]
Answers:
- Square
- Diagonal
- Identity
- Triangular
Fill in the blanks
In this worksheet, students will be given a matrix and asked to fill in the blanks with the correct type of matrix. The four types of matrices are: square, diagonal, identity, and triangular.
Questions:
- A matrix with the same number of rows and columns is called a _____ matrix.
- A matrix with all zeros on the main diagonal and all other entries zeros is called a _____ matrix.
- A matrix with all ones on the main diagonal and all other entries zeros is called a _____ matrix.
- A matrix with all zeros below the main diagonal and all other entries nonzero is called a _____ matrix.
Answers:
- square
- diagonal
- identity
- triangular
True or false
In this worksheet, students will be given a statement about matrices and asked to determine if it is true or false. The statements cover all four types of matrices: square, diagonal, identity, and triangular.
Questions:
- A square matrix can be diagonal.
- A diagonal matrix can be identity.
- An identity matrix is always square.
- A triangular matrix can be square.
- A square matrix can be triangular.
- A triangular matrix can be identity.
- A diagonal matrix cannot be triangular.
- A square matrix cannot be identity.
- A triangular matrix cannot be square.
- An identity matrix cannot be triangular.
Answers:
- True
- True
- True
- True
- True
- True
- True
- False
- False
- False
From The types of matrices to Matrix Course





Responses