Column Matrix – Definition, Examples,Art project & Worksheets

Here we will discuss about the column matrix with examples.
What is a Column Matrix?
A column matrix is a rectangular array of numbers with m rows and 1 column. The elements of a column matrix are written one after the other, with each element in its own row. For example, the following is a column matrix with 3 rows and 1 column:
| 1500 |
| 2200 |
| 1800 |
| 1200 |
Examples of column matrix
Position Vector in 3D Space
A column matrix can represent a position vector in 3D space. Consider a point P(x, y, z). The column matrix representation of this point would be:
| x |
| y |
| z |
Temperature Measurements
Imagine you’re recording temperatures at different times of the day. You can use a column matrix to store these measurements:
| 24.5 |
| 25.0 |
| 23.8 |
| 22.9 |
Color Components in an Image
Consider an image with RGB (Red, Green, Blue) color components. Each pixel’s color can be represented using a column matrix:
| R |
| G |
| B |
Monetary Values
Column matrices can be used to represent monetary values. Let’s say you’re tracking expenses for a week:
| $15.75 |
| $10.50 |
| $30.25 |
| $5.80 |
System of Equations
When solving a system of linear equations, we can use column matrices to represent the coefficients of the variables. For instance, consider the following system:
2x + 3y = 7
4x – y = 1
Harmonizing Music Theory
Imagine a composer crafting a melody. The column matrix emerges, representing musical notes’ frequencies:
| 440 |
| 587 |
| 659 |
| 784 |
The properties of column matrix
A column matrix is a matrix with a single column and an arbitrary number of rows. It is a special case of a matrix, and it has a number of unique properties that set it apart from other types of matrices.
Number of rows
The number of rows in a column matrix is always equal to the number of elements in the column. This is because a column matrix is a matrix with a single column, and the number of rows in a matrix is equal to the number of columns in the matrix. For example, a column matrix with 3 elements will have 3 rows.
Transpose
The transpose of a column matrix is a row matrix. This is because the transpose of a matrix is the matrix that results from swapping the rows and columns. In the case of a column matrix, the rows and columns are the same, so the transpose is simply the matrix itself. For example, the transpose of a column matrix with 3 elements is a row matrix with 3 elements.
Determinant
The determinant of a column matrix is equal to the product of the elements in the column. This is because the determinant of a matrix is the sum of the products of the elements in each row, where each product is multiplied by the sign of the permutation that orders the rows. In the case of a column matrix, there is only one row, so the determinant is simply the product of the elements in the row. For example, the determinant of a column matrix with the elements 1, 2, and 3 is equal to 6.
Orthogonal
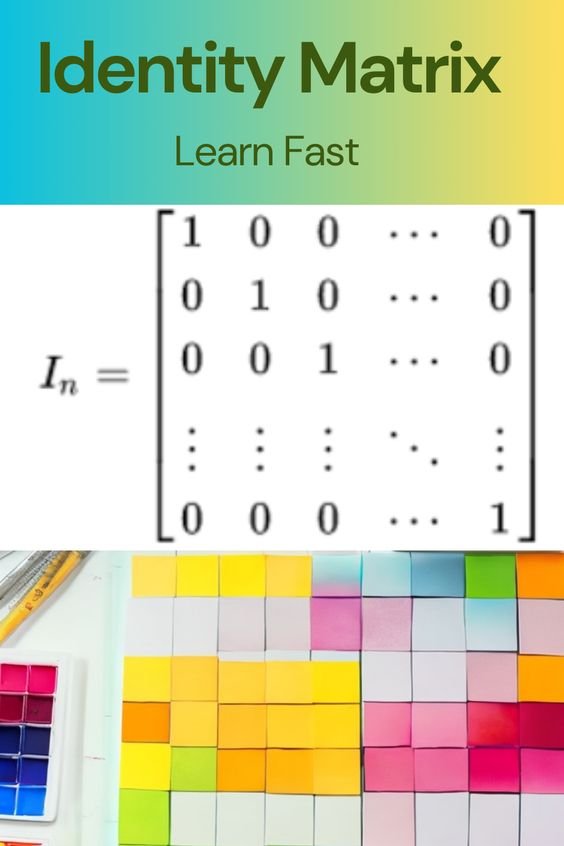
Their product is equal to the identity matrix. This is because the product of two column matrices is simply the sum of the products of the corresponding elements in each matrix. In the case of two column matrices with the same number of elements, the product will be a diagonal matrix with the elements of the matrices on the diagonal. If the matrices are orthogonal, then the diagonal elements will all be equal to 1, and the other elements will be equal to 0.
Column matrices are a useful tool in linear algebra. They can be used to represent vectors, to solve systems of linear equations, and to perform other operations like Computer Graphics,Quantum Mechanics,Economics and Finance.
Fun Activities to Learn Column Matrices Fast
Create a column matrix art project
You can use column matrices to create all sorts of fun and creative art projects. For example, could create a column matrix landscape.
Gather Your Materials
The materials you will need for your column matrix art project will vary depending on the size and complexity of your project. However, you will likely need the following:
- A variety of materials for the columns, such as cardboard tubes, wooden dowels, or plastic straws
- Adhesive to attach the columns together
- A background surface, such as a piece of paper or canvas
- Paint or markers to decorate the columns
Plan Your Column Matrix
Once you have gathered your materials, you can begin to plan your column matrix. Decide on the size and shape of your column matrix, as well as the number of columns you want to use. You may also want to consider the materials you will use for the columns and the background surface.
Assemble Your Column Matrix
Once you have a plan for your column matrix, you can begin to assemble it. Start by attaching the columns together to form the desired shape. You can use hot glue, tape, or another adhesive. Once the columns are attached, you can decorate them with paint or markers.
Add a Background
Once the columns are decorated, you can add a background to your column matrix. You can use a piece of paper or canvas, or you can even create a collage with different materials. The background will help to frame your column matrix and make it look more finished.
Display Your Column Matrix
Once your column matrix art project is complete, you can display it on a wall, table, or shelf. You can also use it as a centerpiece for a table or a focal point in a room. The best way to display your column matrix will depend on the size and shape of your project.
Tips for Creating a Column Matrix Art Project
Use different materials for the columns to create a variety of textures and colors. This will add visual interest to your column matrix.
Get creative with the shape of your column matrix. You can even create a 3D column matrix by attaching the columns to a base. This will make your project more unique and eye-catching.
Use paint or markers to decorate the columns in a way that reflects your personality or interests. This will make your column matrix more personal and meaningful.
Add a background to your column matrix to create a more finished look. This will also help to frame your column matrix and make it look more professional.
Display your column matrix art project in a way that makes it the focal point of a room. This will ensure that your project gets the attention it deserves.

The Height Matrix Game
This game is a great way to help kids learn about column matrices and how they can be used to represent data. To play the game, you will need a column matrix that contains the heights of a group of students. You can either create your own column matrix or find one online.
Once you have a column matrix, you can start the game. The goal of the game is to guess the heights of the students in the column matrix. To do this, you will need to ask the other players questions about the column matrix. For example, you could ask “Is the height of the tallest student in the column matrix greater than 6 feet?” or “Is the average height of the students in the column matrix between 5 and 6 feet?”
The player who guesses the heights of the students in the column matrix correctly wins the game.
The Score Matrix Game
The Score Matrix Game is similar to the Height Matrix Game, but it uses a column matrix to represent the scores of a group of athletes. To play the game, you will need a column matrix that contains the scores of a group of athletes in a particular event. You can either create your own column matrix or find one online.
Once you have a column matrix, you can divide the kids into two teams. The goal of the game is for each team to guess the scores of the athletes in the column matrix. To do this, the teams will take turns asking questions about the column matrix. For example, a team could ask “Is the score of the athlete with the highest score in the column matrix greater than 100?” or “Is the average score of the athletes in the column matrix between 80 and 90?”
The team that guesses the scores of the athletes in the column matrix correctly wins the game.
Tips for playing the Score Matrix Game:
- Make sure the column matrix you use is not too large or too small. A good size for a column matrix is 5-10 athletes.
- Encourage the kids to ask creative questions about the column matrix. The more creative the questions, the more fun the game will be.
- Be prepared to answer questions from the kids about column matrices. This is a great opportunity to teach the kids about column matrices and how they work.
Interesting facts about Column Matrix
In the early days of computer graphics, column matrices were used to represent points and vectors. This made them a convenient way to store and manipulate geometric data. However, it also made them difficult to use for some operations, such as matrix multiplication.
In the 1960s, a mathematician named Jack Dongarra developed a new way to represent points and vectors using column matrices. This new representation, called the “row-major order,” made it much easier to perform matrix multiplication and other operations on column matrices. This led to a revolution in computer graphics, and it is still used today.
Building Bridges
Column matrices find applications in civil engineering, particularly in analyzing the forces in bridges. Engineers use column matrices to represent the forces acting on different parts of a bridge’s structure, helping ensure the bridge’s stability and safety.
Data Transformation
In data science, column matrices are used to represent datasets. Each column of the matrix can represent a different attribute or feature of the data, making it easier to perform operations like data transformations, regressions, and machine learning tasks.
3D Graphics and Transformations
Column matrices play a vital role in 3D graphics. They are used to represent transformations like translation, rotation, and scaling. These transformations are applied to the columns of a matrix to manipulate the position, orientation, and size of objects in a 3D space.
Quantum Mechanics
In quantum mechanics, wave functions are often represented using column matrices. These matrices help describe the probabilities of a particle’s position or state in different quantum states, contributing to the fundamental understanding of quantum behavior.
Economics and Leontief Input-Output Model
The Leontief Input-Output model in economics uses column matrices to represent the consumption and production relationships between different sectors of an economy. This model helps economists analyze the interdependencies within an economy.
Markov Chains
Column matrices are used to represent the state transitions in Markov chains—a concept widely used in various fields, including biology, finance, and computer science. These matrices help model and predict the probability of transitioning from one state to another over time.
Solving Linear Equations
Column matrices are integral to solving systems of linear equations. When expressing a system as a matrix equation, each column matrix corresponds to a variable’s coefficients. By manipulating these matrices, you can efficiently find solutions to complex equations.
Artificial Neural Networks
In machine learning, column matrices often represent the weights connecting nodes in neural networks. These matrices store the parameters that are learned during the training process and play a pivotal role in the network’s ability to make predictions.
Worksheets of column matrix
Questions
1.Introduction to Column Matrices
a.Define a Column Matrix.
b.Create a column matrix.
c.Write the dimensions of the column matrix from question 2.
2.Operations with Column Matrices
Matrix A:
| 4 |
| 2 |
| 9 |
Matrix B:
| 6 |
| 1 |
| 8 |
a.Add matrices A and B. What is the result?
b.Subtract matrix B from matrix A. What is the result?
c.Multiply matrix A by a scalar of 3. Write the resulting matrix.
3.Applications of Column Matrices
Matrix C:
| 2 |
| 5 |
| 3 |
Matrix D:
| 8 |
| 1 |
| 7 |
a.Find the dot product of matrices C and D.
b.Use matrices C and D to represent a system of equations. Write the system.
c.Imagine matrix C represents quantities of items, and matrix D represents their prices. How would you use matrix multiplication to calculate the total cost?
4.Solving Equations with Column Matrices
Solve the system of equations using column matrices:
2x + 3y = 10
5x – y = 3
5.Geometric Transformations
Consider the column matrix representing a point in 2D space:
| 4 |
| 2 |
a.Translate the point by (3, -1).
b.Reflect the point across the y-axis.
c.Rotate the point 90 degrees counterclockwise about the origin.
Answers
1.Introduction to Column Matrices
a.A Column Matrix is a matrix with a single column.
b.| 3 | | 7 | | 1 |
c.3×1 (3 rows, 1 column)
2.Operations with Column Matrices
a.Matrix Result of A + B:
| 10 |
| 3 |
| 17 |
b.Matrix Result of A – B:
| -2 |
| 1 |
| 1 |
c.Matrix Result of 3A:
| 12 |
| 6 |
| 27 |
3.Applications of Column Matrices
a.Dot Product of C and D: 43
b.System of Equations:
2x + 8y = 10
5x + y = 7
c.Total Cost Matrix:
| 41 |
4.Solving Equations with Column Matrices
x = 2, y = 4
5.Geometric Transformations
a.Translated Point: | 7 | | 1 |
b.Reflected Point: | -4 | | 2 |
c.Rotated Point: | -2 | | 4 |
Discover Learn Matrix Fast more ressource at our cool math art store
From Column Matrix to Learn Matrix Fast PAGE





Responses